Question

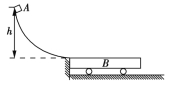
【题目】如图所示，质量为m=2 kg的物块A从高为h=0．2 m的光滑固定圆弧轨道顶端由静止释放，圆弧轨道底端的切线水平，物块A可从圆弧轨道的底端无能量损失地滑上一辆静止在光滑水平面上的小车B，且物块A恰好没有滑离小车B．已知小车B的长度为l=0．75 m，质量M=6 kg，重力加速度为g=10 m/s2，求：

（i）物块A与小车B间的动摩擦因数；

（ii）当物块A相对小车B静止时小车B运动的位移。

Answer 1

【答案】（i） 0．2 （ii） m

【解析】

试题分析： （i）设物块A从圆弧轨道顶端滑到底端时的速度为v0，由动能定理可得mgh=mv02

解得v0==2 m/s

物块A滑上小车B后，系统动量守恒，设它们相对静止时的速度为v，则mv0=（m+M）v

解得v=0．5 m/s

由功能关系可得mv02= （m+M）v2+μmgl

解得μ=0．2

（ii）物块A滑上小车B后，小车B做匀加速运动，小车B的加速度为

它们相对静止时，小车运动的位移为