题目内容
如图所示（1），在竖直平面内有一圆形轨道半径R=0.1m，一质量m=1.0×10-3kg的小球，可在内壁滑动．现在最低点处给小球一个水平初速度v，使小球在竖直平面内逆时针做圆周运动，已知小球始终受到一大小与速度大小成正比、方向沿径向指向圆心的力作用，即F'=kv，其中k为常量．图（2）是小球在竖直平面内做圆周运动的速率v随时间变化的情况，图（3）是小球所受轨道的弹力F随时间变化的情况，已知小球能有两次到达圆形轨道的最高点．结合图象所给数据，g取10m/s2，试求：（1）常量k的值；
（2）小球从开始运动至图中速度为2m/s的过程中，摩擦力对小球做的功．
【答案】分析：（1）由图读出t2时刻小球到达轨道最高点时的速度为2m/s，轨道对小球的弹力为零，由重力和F'的合力提供向心力，根据牛顿第二定律求出k．
（2）t=0时刻，小球开始运动时，由图（3）读出F=8×10-2N，由重力、F′和轨道的弹力F的合力提供向心力，根据牛顿第二定律求出初速度，由动能定理研究小球从开始运动至图中速度为2m/s的过程，得出摩擦力对小球做的功．
解答：解：（1）t2时刻小球到达轨道最高点时v=2m/s，轨道对小球的弹力F=0，根据牛顿第二定律得：
F′+mg=m
又F'=kv，
得到：kv+mg=m
代入解得：k=1.5×10-2Ns/m
（2）t=0时刻，小球开始运动时，由图（3）读出F=8×10-2N，设初速度大小为v，则有：
kv+F-mg=m
代入解得：v=3.5m/s
小球从开始运动至图中速度为2m/s的过程中，指向圆心的力作用F'和轨道对小球的弹力始终不做功，根据动能定理得：
-2mgR+W=
解得：W=-2.125×10-3J
答：（1）常量k为1.5×10-2Ns/m；
（2）小球从开始运动至图中速度为2m/s的过程中，摩擦力对小球做的功为-2.125×10-3J．
点评：本题解题关键是读懂图象，找出图（2）、（3）之间对应的关系．根据动能定理求阻力做功是常用的方法．
（2）t=0时刻，小球开始运动时，由图（3）读出F=8×10-2N，由重力、F′和轨道的弹力F的合力提供向心力，根据牛顿第二定律求出初速度，由动能定理研究小球从开始运动至图中速度为2m/s的过程，得出摩擦力对小球做的功．
解答：解：（1）t2时刻小球到达轨道最高点时v=2m/s，轨道对小球的弹力F=0，根据牛顿第二定律得：
F′+mg=m
又F'=kv，
得到：kv+mg=m
代入解得：k=1.5×10-2Ns/m
（2）t=0时刻，小球开始运动时，由图（3）读出F=8×10-2N，设初速度大小为v，则有：
kv+F-mg=m
代入解得：v=3.5m/s
小球从开始运动至图中速度为2m/s的过程中，指向圆心的力作用F'和轨道对小球的弹力始终不做功，根据动能定理得：
-2mgR+W=
解得：W=-2.125×10-3J
答：（1）常量k为1.5×10-2Ns/m；
（2）小球从开始运动至图中速度为2m/s的过程中，摩擦力对小球做的功为-2.125×10-3J．
点评：本题解题关键是读懂图象，找出图（2）、（3）之间对应的关系．根据动能定理求阻力做功是常用的方法．
练习册系列答案
相关题目
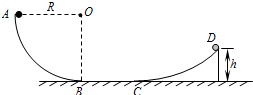如图所示，AB为固定在竖直平面内的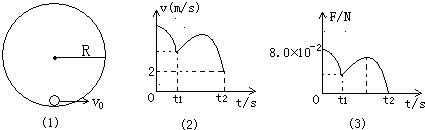
如图所示，ABC为固定在竖直面内的光滑四分之一圆轨道，其半径为r=10m，N为固定在水平面内的半圆平面，其半径为R=