题目内容
（2008?崇明县二模）杂技演员在进行“顶杆”表演时，顶杆演员A顶住一根质量可忽略不计的长竹竿．质量为m=30kg的演员B自竹竿顶部由静止开始下滑，滑到竹竿底端时速度恰好为零．为了研究下滑演员B沿杆的下滑情况，在顶杆演员A与竹竿底部之间安装了一个力传感器．由于竹竿处于静止状态，传感器显示的就是下滑演员B所受摩擦力的情况，如图所示．g=10m/s2．求：（1）下滑演员B下滑过程中的最大速度；
（2）竹杆的长度．
分析：（1）由于摩擦力先小于重力后大于重力，故演员B先加速下滑后减速下滑，根据牛顿第二定律求解加速过程的加速度，再根据速度时间公式计算最大速度；
（2）先求出加速下降的位移，再根据动能定理求出减速下降的位移，两段位移之和即为杆的长度．
（2）先求出加速下降的位移，再根据动能定理求出减速下降的位移，两段位移之和即为杆的长度．
解答：解：（1）以人为研究对象，人加速下滑过程中受重力mg和杆对人的作用力F1，由题图可知，人加速下滑过程中杆对人的作用力F1为180 N．
由牛顿第二定律得
mg-F1=ma，
则a=4 m/s2．
1s末人的速度达到最大，则v=at1=4 m/s．
（2）加速下降时位移为：s1=
at12=2 m．
减速下降时，由动能定理得（mg-F2）s2=0-
mv2，
代入数据解得s2=4m，
杆的长度s=s1+s2=6m．
答：（1）杆上的人下滑过程中的最大速度为4m/s；
（2）竹竿的长度为6m．
由牛顿第二定律得
mg-F1=ma，
则a=4 m/s2．
1s末人的速度达到最大，则v=at1=4 m/s．
（2）加速下降时位移为：s1=
| 1 |
| 2 |
减速下降时，由动能定理得（mg-F2）s2=0-
| 1 |
| 2 |
代入数据解得s2=4m，
杆的长度s=s1+s2=6m．
答：（1）杆上的人下滑过程中的最大速度为4m/s；
（2）竹竿的长度为6m．
点评：本题主要考查了牛顿第二定律及运动学基本公式的直接应用，要求同学们能根据图象得出有效信息，能根据受力情况判断运动情况，难度适中．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
（2008?崇明县二模）一个半径为r、质量为m、电阻为R的金属圆环，用一根长为L的绝缘细绳悬挂于O点，离O点下方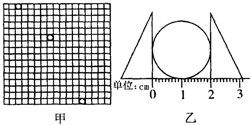
（2008?崇明县二模）如图甲所示，是一位同学在实验室中照的一小球做平抛运动的频闪照片的一部分，由于照相时的疏忽，没有摆上背景方格板，图中方格是后来用直尺画在相片上的（图中格子的竖直线是实验中重垂线的方向，每小格的边长均为5mm ），为了补救这一过失，他对小球的直径进行了测量，如图乙所示，如果取重力加速度 g=10m/s 2，则（1）照片闪光的频率为