题目内容
【题目】如图所示，质量为m的小球用长为L的轻质细线悬于O点，与O点处于同一水平线上的P点处有一根光滑的细钉，已知OP＝L/2，在A点给小球一个水平向左的初速度v0，发现小球恰能到达跟P点在同一竖直线上的最高点B．求：
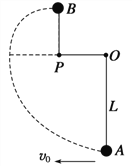
(1)小球到达B点时的速率；
(2)若不计空气阻力，则初速度v0为多少？
(3)若空气阻力不能忽略，则初速度需变为
时才可以恰好到达最高点B，则小球从A到B的过程中克服空气阻力做了多少功？
【答案】（1）
（2）
（3）
【解析】试题分析：（1）小球恰能经过圆弧轨迹的最高点B，在B点由重力提供向心力，由牛顿第二定律有：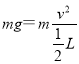 
…①
解得： 
…②
（2）小球从A点运动到B点，只有重力对它做功，根据动能定理有：mg（L+
）＝
mv2
mv02…③
联立②、③两式解得： 
…④
（3）由动能定理可得： 
解得： 
；
练习册系列答案
相关题目
