题目内容
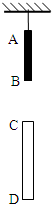
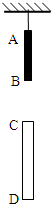 用细绳将木棒AB的A端吊在天花板上,使木棒在竖直方向上静止不动.在A端正下方有一根半透明的玻璃管CD竖直固定在空中,已知点C端距A端1m,管CD长度为0.8m,把细绳轻轻剪断,测得木棒AB通过玻璃管CD的时间间隔为0.4s,重力加速度g=10m/s2,求木棒AB的长度.
用细绳将木棒AB的A端吊在天花板上,使木棒在竖直方向上静止不动.在A端正下方有一根半透明的玻璃管CD竖直固定在空中,已知点C端距A端1m,管CD长度为0.8m,把细绳轻轻剪断,测得木棒AB通过玻璃管CD的时间间隔为0.4s,重力加速度g=10m/s2,求木棒AB的长度.分析:轻杆做自由落体运动,根据自由落体位移公式,分别研究杆下端B到达C点过程和杆上端A到达D点过程,根据位移时间关系公式h=
gt2列式后联立求解即可.
| 1 |
| 2 |
解答:解:设木棒AB的长度为L,B端到达C点的时间为t1,则根据位移时间关系公式h=
gt2,有:
杆下端B到达C点过程:hAC-L=
g
,即:1-L=
×10×
①
杆上端A到达D点过程:hAC+LCD=
g
,即:1+0.8=
×10×
②
△t=t2-t1=0.4s ③
由①②③式解得:L=0.8m;
答:木棒AB的长度为0.8m.
| 1 |
| 2 |
杆下端B到达C点过程:hAC-L=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
| t | 2 1 |
杆上端A到达D点过程:hAC+LCD=
| 1 |
| 2 |
| t | 2 2 |
| 1 |
| 2 |
| t | 2 2 |
△t=t2-t1=0.4s ③
由①②③式解得:L=0.8m;
答:木棒AB的长度为0.8m.
点评:本题关键是明确杆的运动规律,然后选择恰当的过程运用位移时间关系公式列式求解.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
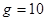
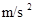 ,求木棒AB的长度。
,求木棒AB的长度。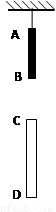
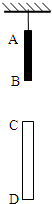 用细绳将木棒AB的A端吊在天花板上,使木棒在竖直方向上静止不动.在A端正下方有一根半透明的玻璃管CD竖直固定在空中,已知点C端距A端1m,管CD长度为0.8m,把细绳轻轻剪断,测得木棒AB通过玻璃管CD的时间间隔为0.4s,重力加速度g=10m/s2,求木棒AB的长度.
用细绳将木棒AB的A端吊在天花板上,使木棒在竖直方向上静止不动.在A端正下方有一根半透明的玻璃管CD竖直固定在空中,已知点C端距A端1m,管CD长度为0.8m,把细绳轻轻剪断,测得木棒AB通过玻璃管CD的时间间隔为0.4s,重力加速度g=10m/s2,求木棒AB的长度.