题目内容
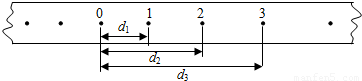
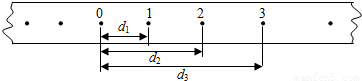
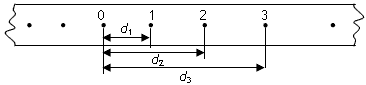
如图，是做匀加速直线运动的小车带动通过打点计时器的纸带的一部分，已知打点周期为T，图中0，1，2，3，4…分别为计时器打下的点，已知2、3点到0点距离分别为d2、d3，则1点到0点间距离d1=| 3d2-d3 |
| 3 |
| 3d2-d3 |
| 3 |
| 1 |
| 2T |
| 4d3 |
| 3 |
| 1 |
| 2T |
| 4d3 |
| 3 |
| 1 |
| T2 |
| 2d3 |
| 3 |
| 1 |
| T2 |
| 2d3 |
| 3 |
分析：根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上2点时小车的瞬时速度大小，根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小．
解答：解：x23=d3-d2，x12=d2-d1，x01=d1，由于匀变速直线运动连续相等的时间间隔内的位移之差为常数，
所以：x23-x12=x12-x01
整理得：d3-d2-d2+d1=d2-d1-d1，
解得：d1=
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，
得：v2=
=
=
(
-d2)
根据匀变速直线运动的推论公式△x=aT2
得：x23-x12=aT2，
整理得：（
-d2）=aT2，
解得：a=
（
-d2）
故答案为：d2-
，
(
-
)，
（
-d2）
所以：x23-x12=x12-x01
整理得：d3-d2-d2+d1=d2-d1-d1，
解得：d1=
| 3d2-d3 |
| 3 |
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，
得：v2=
| x13 |
| 2T |
| d3-d1 |
| 2T |
| 1 |
| 2T |
| 4d3 |
| 3 |
根据匀变速直线运动的推论公式△x=aT2
得：x23-x12=aT2，
整理得：（
| 2d3 |
| 3 |
解得：a=
| 1 |
| T2 |
| 2d3 |
| 3 |
故答案为：d2-
| d3 |
| 3 |
| 1 |
| 2T |
| 4d3 |
| 3 |
| d | 2 |
| 1 |
| T2 |
| 2d3 |
| 3 |
点评：要提高应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
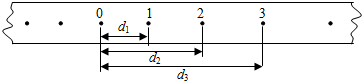如图，是做匀加速直线运动的小车带动通过打点计时器的纸带的一部分，已知打点周期为T，图中0，1，2，3，4…分别为计时器打下的点，已知2、3点到0点距离分别为d2、d3，则1点到0点间距离d1=________，打2点速度v2=________，物体运动的加速度a=________．
