题目内容
如图,水平足够长光滑固定直杆AB上穿有质量为M的滑块,其上用光滑铰链着一个长为L的轻杆,杆的另一端固定着一个质量为M的小球,初始时,系统静止,轻杆水平。
1 给小球以竖直向上的初速v01,球到达最高点时杆与水平方向呈θ角,(θ<900),求v01。
2 给小球以竖直向上的初速v02,球到达最高点时的速度为v,求v02。
![]()
【小题1】![]()
【小题2】![]()
解析:
【小题1】此题中须弄清的几个问题是,小球上升过程中,滑块是向左还是向右运动;小球到达最高点时是否有速度;此时滑块的速度方向如何;我们不妨这样来分析,若没有杆连接,则滑块不动,且小球将竖直向上运动。即最初杆有被拉伸的趋势。则滑块将向左运动。运动中小球和滑块在水平方向上不受外力,所以系统水平方向上动量守恒 ,①问中,假设小球在最高点时有水平向左的速度,则由水平方向动量守恒得滑块将有向右的速度,则上面的分析可知,滑块向左运动中出现向右的速度这是不可能的;若小球在最高点时有向左的速度,则由水平方向动量守恒可知,这时滑块将具有水平向左的速度,二者速度相反,则小球还是要上升,那么此时的位置就不是最高的;若小球具有向上或向下的速度,即小球处于上升或下降的过程中,则小球此时的位置也不是最高的。
![]() ①问中小球在最高点时不可能有速度。即速度为0,则由系统水平方向动量守恒得滑块此时的速度也是0,
①问中小球在最高点时不可能有速度。即速度为0,则由系统水平方向动量守恒得滑块此时的速度也是0,
则由系统机械能守恒(并非小球的机械能守恒)
得 ![]() mv012=mgLsinθ, 解得v01=
mv012=mgLsinθ, 解得v01=![]()
【小题2】2问中小球在最高点时的速度不为0,即小球到达最高点时轻杆竖直且速度向右。
由水平方向动量守恒得
mv-Mvx=0
又由系统机械能守恒![]() mv022=mgL+
mv022=mgL+![]() mv2+
mv2+![]() Mvx2
Mvx2
以上两式联立,可解得v02=![]()

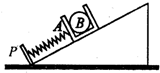 如图,置于足够长斜面上的盒子A内放有光滑球B,B恰与A前、后壁接触,光滑斜面固定于水平地面上,一轻质弹黄的一端与固定在斜面上的木板P连接,另一端与A相连,处于静止状态.今用平行于斜面向下的外力缓慢推A,然后由静止释放,则从释放盒子A直至其获得最大速度的过程中( )
如图,置于足够长斜面上的盒子A内放有光滑球B,B恰与A前、后壁接触,光滑斜面固定于水平地面上,一轻质弹黄的一端与固定在斜面上的木板P连接,另一端与A相连,处于静止状态.今用平行于斜面向下的外力缓慢推A,然后由静止释放,则从释放盒子A直至其获得最大速度的过程中( )| A、弹簧对A做的功等于A机械能的增加量 | B、弹簧的弹性势能一直减小,但并没有减小到零 | C、弹簧弹性势能的减少量等于A和B机械能的增加量 | D、弹簧对A做的功与A所受重力做功的代数和等于A动能的增加量 |
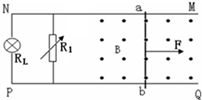 如图,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨放在水平面上,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨电接触良好,金属棒的质量为m、电阻为R.灯泡的电阻RL=3R,调节电阻箱电阻R1=6R,现给金属棒施加水平向右的恒力F,使棒由静止开始运动,试求:
如图,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨放在水平面上,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨电接触良好,金属棒的质量为m、电阻为R.灯泡的电阻RL=3R,调节电阻箱电阻R1=6R,现给金属棒施加水平向右的恒力F,使棒由静止开始运动,试求: 如图,水平放置的光滑平行的金属导轨的间距为L,导轨电阻不计,匀强磁场的磁感应强度B竖直向上,金属杆ab、cd的质量分别为m1、m2,其电阻分别为R1、R2,今使ab杆以初动能Ek沿导轨向左滑出,cd由静止同时释放,导轨足够长,磁场范围足够大,则cd杆产生的电热最大值是
如图,水平放置的光滑平行的金属导轨的间距为L,导轨电阻不计,匀强磁场的磁感应强度B竖直向上,金属杆ab、cd的质量分别为m1、m2,其电阻分别为R1、R2,今使ab杆以初动能Ek沿导轨向左滑出,cd由静止同时释放,导轨足够长,磁场范围足够大,则cd杆产生的电热最大值是 如图,水平放置的光滑导轨间距L=0.5m,空间有垂直纸面向内的匀强磁场B=2T,一根长度也为L的金属棒架在导轨上,以速度V=12m/s向右匀速切割磁感线,设导轨足够长,整个过程金属棒与导轨保持垂直并接触良好,金属棒的电阻r=1Ω,导轨电阻不计,导轨的右侧由电动机M、电阻R以及电容器C组成如图电路,已知电动机线圈内阻R0=0.5Ω,电阻R=2Ω,电阻R上消耗的功率P=8W,电容器C=2μF,试求:
如图,水平放置的光滑导轨间距L=0.5m,空间有垂直纸面向内的匀强磁场B=2T,一根长度也为L的金属棒架在导轨上,以速度V=12m/s向右匀速切割磁感线,设导轨足够长,整个过程金属棒与导轨保持垂直并接触良好,金属棒的电阻r=1Ω,导轨电阻不计,导轨的右侧由电动机M、电阻R以及电容器C组成如图电路,已知电动机线圈内阻R0=0.5Ω,电阻R=2Ω,电阻R上消耗的功率P=8W,电容器C=2μF,试求: