题目内容
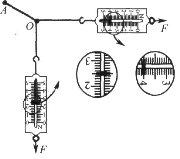
【题目】在“用单摆测重力加速度”的实验中,某同学的操作步骤如下:
a.取一根细线,下端系住直径为![]() cm的金属小球,上端固定在铁架台上;
cm的金属小球,上端固定在铁架台上;
b.用米尺量得固定点到小球上端之间细线的长度![]() cm;
cm;
c.在摆线偏离竖直方向小于![]() 的位置静止释放小球;
的位置静止释放小球;
d.用秒表记录小球完成50次全振动的总时间![]() .
.
(1)根据上述测量数据,可以得到:摆长L为____m;周期T为________s;测得重力加速度![]() _____
_____![]() .
.
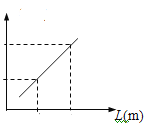
(2)可以通过改变摆长重复实验,测得多组摆长L和对应的周期T的数据,然后以L为横坐标、_______为纵坐标,可以画出如图所示的图线.若图线上选取两个点坐标,求出其“斜率”为K,则由此数据可以算出重力加速度大小为________.
【答案】0.987 1.996 9.769 ![]()
![]()
【解析】
摆线长度与摆球半径之和是单摆的摆长,单摆完成一次全振动需要的时间是单摆的周期,在一个周期内,摆球经过平衡位置两次,根据题意求出单摆的周期;应用单摆周期公式求出重力加速度;根据单摆的周期公式变形得到重力加速度g的表达式,分析T2与L的关系T2-l图线斜率![]() 求出重力加速度大小;
求出重力加速度大小;
【1】(1)摆长为:![]() ;
;
周期![]()
根据![]() 可得:
可得:![]()
【2】)由![]() 得
得![]() ,则然后以L为横坐标、
,则然后以L为横坐标、![]() 为纵坐标,可以画出如图所示的
为纵坐标,可以画出如图所示的![]() 图线,由图可得
图线,由图可得![]() ,可以算出重力加速度大小为
,可以算出重力加速度大小为![]() ;
;

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目