题目内容
1.如图甲所示,M、N为竖直放置的彼此平行的两块平板,两板间的距离为d,两板中央各有一个孔O1、O2,且正对,在两板间有一垂直于纸面方向的磁场,磁感应强度随时间的变化图象 (垂直纸面向里为正)如图乙所示,有一正离子在t=0时刻垂直于M板从小孔O1进入磁场,已知正离子质量为m,带电量为q,正离子在磁场中做匀速圆周运动的周期为T0,速度为v0=$\frac{4πd}{5{T}_{0}}$(不考虑磁场变化而产生的电场的影响,不计正离子所受重力,其中m,q,π,d,T0为已知量).求: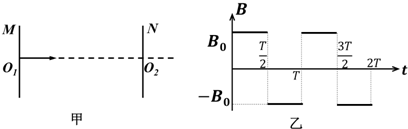
(1)磁感应强度B0的大小;
(2)若磁感应强度随时间变化的周期也为T0,正离子从$\frac{T}{4}$时刻开始进入,则打到N板上离O2点的距离;
(3)若正离子从$\frac{T}{2}$时刻进入,在以后的运动过程中不会打到M板,则磁感应强度随间变化的周期T满足什么条件?
分析 (1)根据牛顿第二定律,由洛伦兹力提供向心力,结合圆周运动的周期公式,可求出磁感应强度.
(2)求出半径,画出运动的轨迹,然后结合几何关系,从而求出打到N板上离O2点的距离;
(3)若恰好不会打到M板,画出运动的轨迹图,然后结合几何关系即可正确解答.
解答 解:(1)正离子射入磁场,洛伦兹力提供向心力有:${B}_{0}q{v}_{0}=m\frac{{v}_{0}^{2}}{R}$
做匀速圆周运动的周期为:${T}_{0}=\frac{2πR}{{v}_{0}}$
联立两式得磁感应强度为:${B}_{0}=\frac{2πm}{q{T}_{0}}$
(2)要使正离子从O′孔垂直于N板射出磁场,v0的方向向右,
离子运动的半径:$R=\frac{m{v}_{0}}{q{B}_{0}}=\frac{m•\frac{4πd}{5{T}_{0}}}{q•\frac{2πm}{q{T}_{0}}}=\frac{2}{5}d$
由左手定则可知,正离子从$\frac{T}{4}$时刻开始进入,受到的洛伦兹力的方向向上,经过$\frac{T}{4}$后,离子转过$\frac{1}{4}$周期,偏转角是90°,所以速度的方向竖直向上;之后由于磁场的方向反向,所以受到的洛伦兹力的方向反向,离子向右偏转,直到打在N板上,如图:
由图可知,$\overline{OA}=d-2R=d-2×\frac{2}{5}d=\frac{1}{5}d=\frac{1}{2}R$
则由几何关系可得:$\overline{AB}=\sqrt{{R}^{2}-{\overline{OA}}^{2}}=\frac{\sqrt{3}}{2}R=\frac{\sqrt{3}}{5}d$,
打到N板上离O2点的距离:
$\overline{{O}_{2}B}=R+\overline{AB}=\frac{2+\sqrt{3}}{5}d$
(3)若正离子从$\frac{T}{2}$时刻进入,在以后的运动过程中若恰好不会打到M板,则运动的轨迹如图: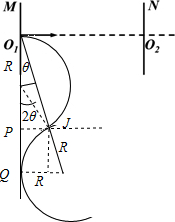
由图中几何关系可得:
(2Rcosθ+R)sinθ=R
(或:Rsin2θ=R(1-sinθ))
整理得:θ≈20°
此时在$\frac{T}{2}$时间内粒子偏转的角度为(180°-2×20°)=140°,所以:
$\frac{\frac{1}{2}T}{\frac{1}{2}{T}_{0}}=\frac{140°}{180°}=\frac{7}{9}$
即:$T=\frac{7}{9}{T}_{0}$
若以后的运动过程中不会打到M板,则离子在半个周期内转过的角度不能大于140°,即$T≤\frac{7}{9}{T}_{0}$
答:(1)磁感应强度B0的大小是$\frac{2πm}{q{T}_{0}}$;
(2)若磁感应强度随时间变化的周期也为T0,正离子从$\frac{T}{4}$时刻开始进入,则打到N板上离O2点的距离是$\frac{2+\sqrt{3}}{5}d$;
(3)若正离子从$\frac{T}{2}$时刻进入,在以后的运动过程中不会打到M板,则磁感应强度随间变化的周期T满足条件$T≤\frac{7}{9}{T}_{0}$.
点评 该题考查离子在洛伦兹力作用下做匀速圆周运动,掌握牛顿第二定律的应用,理解几何关系的运用,同时注意运动的周期性以及离子运动的轨迹图的画法.

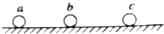 如图所示,光滑绝缘水平面上,a,b,c三球在库伦力作用下保持静止,现把b球电荷量减小一半,保持三球位置不变使三球仍在库伦力作用下静止,则a,b,c两球的电荷量变化为(三球均可看做点电荷)( )
如图所示,光滑绝缘水平面上,a,b,c三球在库伦力作用下保持静止,现把b球电荷量减小一半,保持三球位置不变使三球仍在库伦力作用下静止,则a,b,c两球的电荷量变化为(三球均可看做点电荷)( )| A. | a球电荷量加倍,c球电荷量减半 | B. | a球电荷量加倍,c球电荷量加倍 | ||
| C. | a球电荷量减半,c球电荷量减半 | D. | a球电荷量减半,c球电荷量加倍 |
| A. | 玛丽居里首先提出原子的核式结构学说 | |
| B. | 汤姆生通过对阴极射线的研究发现了电子,从而证明了原子核可再分 | |
| C. | 普朗克在1900年把能量子引入物理学,正确地破除了“能量连续变化”的传统观念 | |
| D. | 爱因斯坦为解释光电效应的实验规律提出了光子说 |
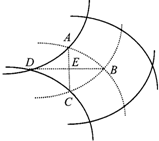 如图表示两列频率相同的水波在某时刻叠加后发生稳定干涉的图样,图中实线表示波峰,虚线表示波谷,已知两列波的振幅相等,下列说法正确的是( )
如图表示两列频率相同的水波在某时刻叠加后发生稳定干涉的图样,图中实线表示波峰,虚线表示波谷,已知两列波的振幅相等,下列说法正确的是( )| A. | B、D两质点振动始终是加强的 | B. | B、D两点的位移始终最大 | ||
| C. | A、C两质点振动始终是加强的 | D. | A、C两质点的位移始终为0 |
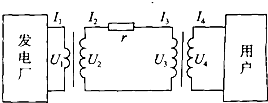 如图所示为远距离交流输电的简化电路图.在发电厂与输电线间连有一理想升压变压器,用等效总电阻是r的两条输电线输电,在输电线与用户间连有一理想降压变压器,则( )
如图所示为远距离交流输电的简化电路图.在发电厂与输电线间连有一理想升压变压器,用等效总电阻是r的两条输电线输电,在输电线与用户间连有一理想降压变压器,则( )| A. | 输电线路上电流I2=$\frac{{U}_{2}}{r}$ | |
| B. | 根据P=$\frac{{{U}_{2}}^{2}}{r}$,提高U2,输电线路上损失的电功率变大 | |
| C. | 升压理想变压器的输入功率为P1=I22r | |
| D. | 输电线路上损失的电功率为I2(U2-U3) |

| A. | 两球的向心加速度大小之比为1:$\sqrt{3}$ | B. | 两球做圆运动的半径之比为1:1 | ||
| C. | 两球的线速度大小之比为1:$\sqrt{2}$ | D. | 两球离地面的高度之比为1:3 |
 如图所示,可视为质点的总质量(包括装备)为m=60kg的滑板运动员,从高为H=15m的斜面AB的顶端A点由静止开始沿斜面下滑,在B点进入光滑的四分之一圆弧BC,圆弧BC半径为R=5m,运动员经C点沿竖直轨道冲出向上运动,经时间t=2s后又落回轨道.若运动员经C点后在空中运动时只受重力,轨道AB段粗糙、BC段光滑.g=10m/s2.(不计过B点时机械能的损耗)求:
如图所示,可视为质点的总质量(包括装备)为m=60kg的滑板运动员,从高为H=15m的斜面AB的顶端A点由静止开始沿斜面下滑,在B点进入光滑的四分之一圆弧BC,圆弧BC半径为R=5m,运动员经C点沿竖直轨道冲出向上运动,经时间t=2s后又落回轨道.若运动员经C点后在空中运动时只受重力,轨道AB段粗糙、BC段光滑.g=10m/s2.(不计过B点时机械能的损耗)求: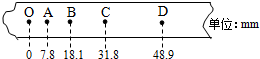 “验证机械能守恒定律”的实验采用重物自由下落的方法:
“验证机械能守恒定律”的实验采用重物自由下落的方法: