题目内容
在“极限”运动会中,有一个在钢索桥上的比赛项目.如图所示,总长为L的均匀粗钢丝绳固定在等高的A、B处,钢丝绳最低点与固定点A、B的高度差为打,动滑轮起点在A处,并可沿钢丝绳滑动,钢丝绳最低点距离水面也为H.若质量为m的参赛者抓住滑轮下方的挂钩由A点静止滑下,最远能到达右侧C点,C、B间钢丝绳相距为L′=
,高度差为h=
.参赛者在运动过程中视为质点,滑轮受到的阻力大小可认为不变,且克服阻力所做的功与滑过的路程成正比,不计参赛者在运动中受到的空气阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变.重力加速度为g.求:

(1)滑轮受到的阻力大小;
(2)若参赛者不依靠外界帮助要到达召点,则参赛者在A点处抓住挂钩时至少应该具有的初动能;
(3)某次比赛规定参赛者须在钢丝绳最低点松开挂钩并落到与钢丝绳最低点水平相距为4a、宽度为a、厚度不计的海绵垫子上.若参赛者由A点静止滑下,会落在海绵垫子左侧的水中.为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围.
| L |
| 10 |
| H |
| 3 |

(1)滑轮受到的阻力大小;
(2)若参赛者不依靠外界帮助要到达召点,则参赛者在A点处抓住挂钩时至少应该具有的初动能;
(3)某次比赛规定参赛者须在钢丝绳最低点松开挂钩并落到与钢丝绳最低点水平相距为4a、宽度为a、厚度不计的海绵垫子上.若参赛者由A点静止滑下,会落在海绵垫子左侧的水中.为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围.
分析:(1)对A到C段运用动能定理,求出滑轮受到的阻力大小.
(2)对A到B点运用动能定理,求出参赛者在A点处抓住挂钩时至少应该具有的初动能.
(3)根据平抛运动的规律求出参赛者做平抛运动的初速度的范围,结合动能定理求出参赛者在A点抓住挂钩时应具有初动能的范围.
(2)对A到B点运用动能定理,求出参赛者在A点处抓住挂钩时至少应该具有的初动能.
(3)根据平抛运动的规律求出参赛者做平抛运动的初速度的范围,结合动能定理求出参赛者在A点抓住挂钩时应具有初动能的范围.
解答:解:(1)设滑轮受到的阻力为Ff,根据动能定理得,
mgh-Ff(L-L′)=0
由L′=
,h=
得滑轮受到的阻力Ff=
.
(2)设参赛者在A点处抓住挂钩时至少具有的初动能为Ek0,根据动能定理,参赛者在A到B的过程中有
-FfL=0-Ek0
Ek0=
mgH .
(3)参赛者落到海绵垫子的过程做平抛运动.设参赛者脱离挂钩时的速度为v,运动的水平位移为s,则
s=vt
H=
gt2
t=
.
当s=4a时,参赛者具有的最小速度为vmin=
.
当s=5a时,参赛者具有的最大速度为vmax=
.
设参赛者在A点抓住挂钩的初动能为Ek,由动能定理,参赛者在A点到钢索最低点的运动过程中有:
mgH-Ff
=
mv2-Ek
由此可得,参赛者在A点抓住挂钩的最小和最大初动能分别为:
Emin=
-
mgH
Emax=
-
mgH
则初动能范围为:
-
mgH<E<
-
mgH.
答:(1)滑轮受到的阻力大小为Ff=
.
(2)参赛者在A点处抓住挂钩时至少应该具有的初动能Ek0=
mgH .
(3)参赛者在A点抓住挂钩时应具有初动能的范围
-
mgH<E<
-
mgH.
mgh-Ff(L-L′)=0
由L′=
| L |
| 10 |
| H |
| 3 |
得滑轮受到的阻力Ff=
| 10mgH |
| 27L |
(2)设参赛者在A点处抓住挂钩时至少具有的初动能为Ek0,根据动能定理,参赛者在A到B的过程中有
-FfL=0-Ek0
Ek0=
| 10 |
| 27 |
(3)参赛者落到海绵垫子的过程做平抛运动.设参赛者脱离挂钩时的速度为v,运动的水平位移为s,则
s=vt
H=
| 1 |
| 2 |
t=
|
当s=4a时,参赛者具有的最小速度为vmin=
| 2a |
| H |
| 2gH |
当s=5a时,参赛者具有的最大速度为vmax=
| 5a |
| 2H |
| 2gH |
设参赛者在A点抓住挂钩的初动能为Ek,由动能定理,参赛者在A点到钢索最低点的运动过程中有:
mgH-Ff
| L |
| 2 |
| 1 |
| 2 |
由此可得,参赛者在A点抓住挂钩的最小和最大初动能分别为:
Emin=
| 4mga2 |
| H |
| 22 |
| 27 |
Emax=
| 25mga2 |
| 4H |
| 22 |
| 27 |
则初动能范围为:
| 4mga2 |
| H |
| 22 |
| 27 |
| 25mga2 |
| 4H |
| 22 |
| 27 |
答:(1)滑轮受到的阻力大小为Ff=
| 10mgH |
| 27L |
(2)参赛者在A点处抓住挂钩时至少应该具有的初动能Ek0=
| 10 |
| 27 |
(3)参赛者在A点抓住挂钩时应具有初动能的范围
| 4mga2 |
| H |
| 22 |
| 27 |
| 25mga2 |
| 4H |
| 22 |
| 27 |
点评:本题考查了动能定理的综合运用,运用动能定理解题关键选择研究过程,分析过程中有哪些力做功,通过定能定理列式求解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

 的均匀粗钢丝绳固定在等高的
的均匀粗钢丝绳固定在等高的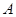 、
、 处,钢丝绳最低点与固定点
处,钢丝绳最低点与固定点 ,动滑轮起点在
,动滑轮起点在 的人抓住滑轮下方的挂钩由
的人抓住滑轮下方的挂钩由 点,
点,
 ,高度差为
,高度差为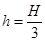 .若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为
.若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为 ,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的空气阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变.
,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的空气阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变.
 、宽度为
、宽度为 ,厚度不计的海绵垫子上.若参赛者由
,厚度不计的海绵垫子上.若参赛者由 ,高度差为
,高度差为 。若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为
。若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为 ,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变。
,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变。
 、宽度为
、宽度为 ,厚度不计的海绵垫子上。若参赛者由A点静止滑下,会落在海绵垫子左侧的水中。为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围?
,厚度不计的海绵垫子上。若参赛者由A点静止滑下,会落在海绵垫子左侧的水中。为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围?