题目内容
9. 2015年3月11日,世青赛女子组平行大回转赛况中,俄罗斯选手索博列娃获得该项目冠军,如图所示,假设该滑雪运动员从R=18m的$\frac{1}{4}$圆弧轨道AB段加速,经水平滑道BC,再在C点飞出水平轨道后做出美丽的空中动作,最后落至D点.运动员质量m=60kg,经过AB段加速滑行后进入BC轨道过程中没有能量损失,BC段运动员的运动时间t=0.6s,运动员滑板与轨道件摩擦因数μ=0.5,求:
2015年3月11日,世青赛女子组平行大回转赛况中,俄罗斯选手索博列娃获得该项目冠军,如图所示,假设该滑雪运动员从R=18m的$\frac{1}{4}$圆弧轨道AB段加速,经水平滑道BC,再在C点飞出水平轨道后做出美丽的空中动作,最后落至D点.运动员质量m=60kg,经过AB段加速滑行后进入BC轨道过程中没有能量损失,BC段运动员的运动时间t=0.6s,运动员滑板与轨道件摩擦因数μ=0.5,求:(1)若在由圆轨道进入水平轨道之间对B点的压力是体重的2.8倍,则AB段运动员克服摩擦力的功是多少?
(2)若轨道BC比D点高H=20m,离开C点后不计空气阻力,则落地点D距B点的水平距是多少?
分析 (1)在B点,应用牛顿第二定律求出运动员的速度,然后应用动能定理求出在AB克服摩擦力做的功.
(2)由动量定理可以求出运动员到达C点的速度,运动员离开水平轨道后做平抛运动,应用平抛运动规律可以求出水平位移.
解答 解:(1)在B点,由牛顿第二定律得:F-mg=m$\frac{{v}_{B}^{2}}{R}$,
由题意可知:F=2.8mg,
代入数据解得:vB=18m/s,
运动员从A到B过程,由动能定理得:mgR-W=$\frac{1}{2}$mvB2-0,
代入数据解得:W=1080J;
(2)以向右为正方向,从B到C过程,由动量定理得:
-μmgtBC=mvC-mvB,
代入数据解得:vC=15m/s,
sBC=$\frac{{v}_{B}+{v}_{C}}{2}$t=$\frac{18+15}{2}$×0.6=9.9m,
运动员离开BC后做平抛运动,
在竖直方向:H=$\frac{1}{2}$gt2,
代入数据解得:t=2s,
水平方向:s=vCt,
代入数据解得:s=30m,
xDB=sBC+s=39.9m;
答:(1)AB段运动员克服摩擦力的功是1080J.
(2)落地点D距B点的水平距是39.9m.
点评 本题是一道力学综合题,分析求出运动员的运动过程是正确解题的前提与关键,分析清楚运动过程后,应用牛顿第二定律、动能定理、平抛运动规律可以解题.

练习册系列答案
相关题目
19.三个相同的灯泡A、B、C连成如图所示的电路,当变阻器的滑动触头P向上移动时( )

| A. | A灯变亮,B灯变暗,C灯变亮 | B. | A灯变亮,B灯和C灯都变暗 | ||
| C. | 电源的总电功率减小 | D. | A灯与B灯亮度相同 |
4. 如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )
如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )
 如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )
如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )| A. | 两次移动时电荷在初位置的加速度之比为10:1 | |
| B. | 两次移动过程电场力做功之比为1:1 | |
| C. | 移动过程中末速度之比为$\sqrt{10}$:1 | |
| D. | 导体上右端点A的电势等于左端点B的电势 |
3.矩形线圈在匀强磁场中匀速转动产生的电动势如图示,则( )


| A. | t1时刻线圈中磁通量为零 | B. | t2时刻线圈中磁通量变化率最大 | ||
| C. | t3时刻线圈中磁通量变化率最大 | D. | t4时刻线圈面与磁场方向垂直 |
10.下列关于地球同步通讯卫星的说法中正确的是( )
| A. | 所有同步通讯卫星的周期都是24h | |
| B. | 所有同步通讯卫星必须定点在地球赤道上空某处 | |
| C. | 不同的同步通讯卫星的轨道半径一般是不同的 | |
| D. | 不同的同步通讯卫星运行的线速度大小是相同的,但加速度的大小可能不同 |
7. 如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )
如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )
 如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )
如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )| A. | 初速度更大 | B. | 加速度更大 | ||
| C. | 动能增量更大 | D. | 两次的电势能增量相同 |
8.下列关于离心现象的说法正确的是( )
| A. | 做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将沿切线做直线运动 | |
| B. | 当物体所受的离心力大于向心力时产生离心现象 | |
| C. | 做匀速圆周运动的物体,当它所受的一切力都消失时,它将做背离圆心的圆周运动 | |
| D. | 做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将做曲线运动 |
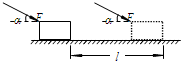 如图所示,质量为m的物块在与水平方向成α角的恒定推力F的作用下,由静止沿水平面向右运动一段距离l时,速度为v.在此过程中,恒力F对物块所做的功为Flcosα,重力做功为0,摩擦力做功为$\frac{1}{2}$mv2-Flcosα.速度为v时推力F的功率为Fvcosα.
如图所示,质量为m的物块在与水平方向成α角的恒定推力F的作用下,由静止沿水平面向右运动一段距离l时,速度为v.在此过程中,恒力F对物块所做的功为Flcosα,重力做功为0,摩擦力做功为$\frac{1}{2}$mv2-Flcosα.速度为v时推力F的功率为Fvcosα.