��Ŀ����
18�������¿ɹ�ѡ�õ�ʵ�����ļ�������������Ҫ���ܾ�ȷ�ز������������������ƫ���������̣���A�����������A0����ƫ����ԼΪ700?A��800?A���ڵ���ԼΪ100������֪�����ϵĿ̶Ⱦ������ܸ���ΪN
B��������A������Ϊ0.6A���ڵ���Ϊ0.1�� C����ѹ��V������Ϊ3V���ڵ���Ϊ3K��
D������������R�������ֵΪ200�� E����ԴE���綯��ԼΪ3V���ڵ���Ϊ1.5��
F������Sһֻ
��1�����������Ҫ����B��������A���͡�C����ѹ��V����Ӧѡ��C�����B����C����
��2�������߿��ڻ�������Ƶ�ʵ���·ͼ��
��3�����������У�����������ݣ�����һ�������д��������A0��ָ��ƫת��n�ɼ������ƫ����Im=$\frac{NU}{n{R}_{v}}$��ʽ�г�N��n�⣬������ĸ���Ŵ�������������UΪ��ѹ��ʾ����RV��ѹ�����裮
���� ��1��2����ѹ������3V������3K������ƫ����ΪIg=$\frac{3}{3000}$A=1mA���������������ƣ����Ե���������ʹ�ã����û�����������ѹʽ�ӷ�����ѹ�����������ڣ�
��3������ŷķ����������ѹ���������õ�ͨ������������ĵ������������̶Ⱦ��ȣ�ÿС���ʾ�ĵ�����ȣ����ݱ�����ϵ��ʽ���������������ƫ������
��� �⣺��1����ѹ������3V������3K������ƫ����ΪIg=$\frac{3}{3000}$A=1mA=1000��A���������������ƣ����Ե���������ʹ�ã������������������ɣ�
��Ŀ�еĵ���������0.6����ƫ����Ҫ����Ӧѡ�õ�ѹ��C��
��2����ʵ����û�����������ѹʽ�ӷ�����ѹ�����������ڣ�
��·ͼ��ͼ��ʾ��
��3������������ܸ���ΪN���������ڵ�ѹ��������Ϊ��I=$\frac{U}{{R}_{V}}$��
���������ѹ��������ͨ�����ǵĵ���I��ȣ�ָ��ƫת����֮�ȣ�n��N=I��Ig��
��Ig=$\frac{NI}{n}$=$\frac{NU}{n{R}_{V}}$��UΪ��ѹ��������RVΪ��ѹ�����裻
�ʴ�Ϊ����1��C����2����ͼ��ʾ����3��$\frac{NU}{n{R}_{V}}$��UΪ��ѹ��������RVΪ��ѹ�����裮
���� ����ؼ�����ȷʵ��ԭ����֪����ѹ���൱�ڴ����裬�ܹ����ŷķ������ʽ������
Ӧ��ȷ���ٵ���ķ�����ӷ�������ѹ������ƫ�������������ӽ�ʱ��Ӧ���ǽ���ѹ����������������������������ƫ��ѹ������ѹ��ͬʱ��Ӧ���ǽ�������������·�������ڵ���������ȫ����ԶС�ڴ����·�ĵ���ʱ��������Ӧ���÷�ѹʽ�ӷ���

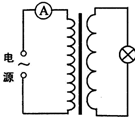 ��ͼ��ʾ�������ѹ��ԭ������Ȧ����֮��Ϊ10��1��ԭ��Ȧ����Ƶ��Ϊ50Hz�����ҽ�����Դ�ϣ����ӵĵ�����Ϊ���������������Ȧ���롰220V 60W������һֻ����ʱ�����������⣮�ɴ˿�֪��������
��ͼ��ʾ�������ѹ��ԭ������Ȧ����֮��Ϊ10��1��ԭ��Ȧ����Ƶ��Ϊ50Hz�����ҽ�����Դ�ϣ����ӵĵ�����Ϊ���������������Ȧ���롰220V 60W������һֻ����ʱ�����������⣮�ɴ˿�֪��������| A�� | ��������ʾ��ԼΪ0.27A | B�� | ԭ��Ȧ���˵�ѹ���ֵΪ2200$\sqrt{2}$V | ||
| C�� | ��Դ���������Ϊ6W | D�� | ����Ȧ�н��������Ƶ��Ϊ5Hz |
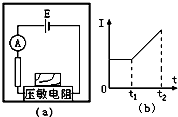 ѹ���������ֵ��������ѹ�����������С�����������н��������ѹ�������ϣ�ѹ�����������ͼ��a����ʾ�ĵ�·�У���������ʾ���仯�����ͼ��b����ʾ��ijͬѧ���ݵ�������ʾ���仯����ƶ����������˶�����������ƶ���ȷ���ǣ�������
ѹ���������ֵ��������ѹ�����������С�����������н��������ѹ�������ϣ�ѹ�����������ͼ��a����ʾ�ĵ�·�У���������ʾ���仯�����ͼ��b����ʾ��ijͬѧ���ݵ�������ʾ���仯����ƶ����������˶�����������ƶ���ȷ���ǣ�������| A�� | 0-t1ʱ���ڣ�������һ�������˶� | |
| B�� | 0-t1ʱ���ڣ����������ܼ������� | |
| C�� | t1-t2ʱ���ڣ������������������� | |
| D�� | t1-t2ʱ���ڣ������������ȼ������� |
| A�� | �Ƹ���������������ǵ��ٶ��ǵ�����������ٶȵ�$\frac{k}{n}$ | |
| B�� | ������������ǵ���������$\frac{{k}^{3}}{{n}^{2}}$ | |
| C�� | �����������������ٶ��ǵ��������������ٶȵ�$\frac{k}{{n}^{2}}$ | |
| D�� | ��������ܶ��ǵ����ܶȵ�$\frac{k}{{n}^{2}}$ |
 ijͬѧ������ͼ��ʾ��װ��̽�������ٶȱ仯�Ĺ�ϵ��
ijͬѧ������ͼ��ʾ��װ��̽�������ٶȱ仯�Ĺ�ϵ��
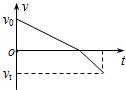
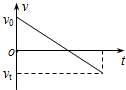
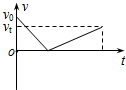
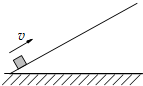 ��ͼ��ʾ��һ�����Գ��ٶ�v0�Թ̶��ڵ����б��˳���б�棬����ijһ�߶Ⱥ��ַ��صˣ�ȡ��б������Ϊ���������б�ʾ������б���������˶��������ٶ�v��ʱ��t�仯��ͼ���У�������ȷ���ǣ�������
��ͼ��ʾ��һ�����Գ��ٶ�v0�Թ̶��ڵ����б��˳���б�棬����ijһ�߶Ⱥ��ַ��صˣ�ȡ��б������Ϊ���������б�ʾ������б���������˶��������ٶ�v��ʱ��t�仯��ͼ���У�������ȷ���ǣ�������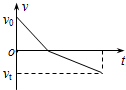
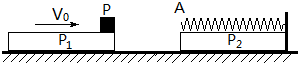 ��ͼ��ʾ��������ͬƽ��P1��P2���ڹ⻬ˮƽ���ϣ�������Ϊm��P2���Ҷ˹̶�һ���ʵ��ɣ����ɵ����ɶ�ǡ����P2�����A�㣮����P����P1�����Ҷˣ�����Ϊ2m�ҿ��Կ����ʵ㣮P1��P�Թ�ͬ�ٶ�v0�����˶����뾲ֹ��P2������ײ����ײʱ�伫�̣���ײ��P1��P2ճ����һ��Pѹ�����ɺ��ز�ͣ��A�㣨����ʼ���ڵ������ڣ���P��P2֮��Ķ�Ħ������Ϊ�̣���
��ͼ��ʾ��������ͬƽ��P1��P2���ڹ⻬ˮƽ���ϣ�������Ϊm��P2���Ҷ˹̶�һ���ʵ��ɣ����ɵ����ɶ�ǡ����P2�����A�㣮����P����P1�����Ҷˣ�����Ϊ2m�ҿ��Կ����ʵ㣮P1��P�Թ�ͬ�ٶ�v0�����˶����뾲ֹ��P2������ײ����ײʱ�伫�̣���ײ��P1��P2ճ����һ��Pѹ�����ɺ��ز�ͣ��A�㣨����ʼ���ڵ������ڣ���P��P2֮��Ķ�Ħ������Ϊ�̣���