题目内容
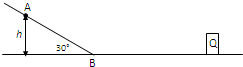如图所示，一倾角为30°的光滑斜面与水平地面平滑连接，水平地面的动摩擦因数为0.25，前方距离斜面底端B点10m处有一个障碍物Q．现有一小孩从斜面上h=3m高处的A点由静止开始滑下，不计小孩到斜面底端时受到的冲击（即到达B点前后瞬间速度大小不变），取g=10m/s2，试回答下列问题：（1）小孩到达斜面底端时的速度大小是多少？
（2）试通过计算判断，小孩会不会碰到障碍物？
（3）接上述第（2）问，若不碰到障碍物，则小孩停在水平面上的位置距离障碍物有多远？若会碰到障碍物，则为了安全，小孩从斜面上静止开始下滑的高度不得超过多少？
分析：（1）斜面光滑，小孩在斜面下滑过程中，只有重力做功，机械能守恒，可列式求解小孩到达斜面底端时的速度大小．
（2）对于小孩运动的全过程，运用动能定理求出小孩能滑行的最大距离，即可判断小孩会不会碰到障碍物．
（3）小孩刚好碰到障碍物时到达障碍物处的速度恰好为零，对整个过程，运用动能定理求解．
（2）对于小孩运动的全过程，运用动能定理求出小孩能滑行的最大距离，即可判断小孩会不会碰到障碍物．
（3）小孩刚好碰到障碍物时到达障碍物处的速度恰好为零，对整个过程，运用动能定理求解．
解答：解：（1）小孩在斜面下滑过程中，只有重力做功，机械能守恒，则得：
mgh=
mv2
则得：小孩到达斜面底端时的速度大小 v=
=
m/s=2
m/s；
（2）设小孩能滑行的最大距离为s．
对于小孩运动的全过程，运用动能定理得：
mgh-μmgs=0
则得：s=
=
m=12m
可见，s大于B点与障碍物间的距离，所以小孩会碰到障碍物．
（3）为了安全，设小孩从斜面上静止开始下滑的最大高度为H．
对整个过程，运用动能定理得：
mgH-μmgsBQ=0
解得：H=μsBQ=0.25×10m=2.5m
答：
（1）小孩到达斜面底端时的速度大小是2
m/s．
（2）小孩会碰到障碍物．
（3）为了安全，小孩从斜面上静止开始下滑的高度不得超过2.5m．
mgh=
| 1 |
| 2 |
则得：小孩到达斜面底端时的速度大小 v=
| 2gh |
| 2×10×3 |
| 15 |
（2）设小孩能滑行的最大距离为s．
对于小孩运动的全过程，运用动能定理得：
mgh-μmgs=0
则得：s=
| h |
| μ |
| 3 |
| 0.25 |
可见，s大于B点与障碍物间的距离，所以小孩会碰到障碍物．
（3）为了安全，设小孩从斜面上静止开始下滑的最大高度为H．
对整个过程，运用动能定理得：
mgH-μmgsBQ=0
解得：H=μsBQ=0.25×10m=2.5m
答：
（1）小孩到达斜面底端时的速度大小是2
| 15 |
（2）小孩会碰到障碍物．
（3）为了安全，小孩从斜面上静止开始下滑的高度不得超过2.5m．
点评：本题涉及力在空间的效果，优先考虑选择动能定理，比较简便，也可以根据牛顿第二定律和运动学公式结合求解．
练习册系列答案
阅读快车系列答案
相关题目
（2010?闵行区三模）如图所示，一倾角为37°的斜面固定在水平地面上，质量m=1kg的物体在平行于斜面向上的恒力F作用下，从A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达C点时速度为零．每隔0.2s通过速度传感器测得物体的瞬时速度，下表给出了部分测量数据．（取 sin37°=0.6．cos37°=0.8）试求：
（2011?普陀区二模）如图所示，一倾角为37°的斜面固定在水平地面上，质量为1千克的物体在平行于斜面向上的恒力F作用下，从斜面的底端A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达最高点C．每隔0.2s通过位移传感器测得物体的瞬时速度的大小，下表给出了部分测量数据．（取sin37°=0.6，cos37°=0.8）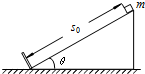
如图所示，一倾角为θ=37°的光滑斜面固定在地面上，斜面长度s0=3.0m，斜面底端有一垂直于斜面的固定挡板．在斜面顶端由静止释放一质量m=0.10kg的小物块．当小物块与挡板第一次碰撞后，能沿斜面上滑的最大距离s=0.75m．已知小物块第一次与挡板碰撞过程中从接触到离开所用时间为0.10s，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8．求：
,sin37o=0.6,cos37o=0.8.）求：