题目内容
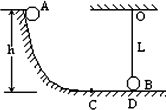
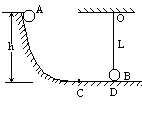
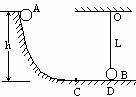
 如图所示,球A无初速地沿光滑圆弧滑下至最低点C后,又沿水平轨道前进至D与质量、大小完全相同的球B发生动能没有损失的碰撞,碰撞后两球交换速度.B球用长L的细线悬于O点,恰与水平地面切于D点.A球与水平地面间摩擦系数??=0.1,已知球A初始高度h=2m,CD=1m,g取10m/s2.问:
如图所示,球A无初速地沿光滑圆弧滑下至最低点C后,又沿水平轨道前进至D与质量、大小完全相同的球B发生动能没有损失的碰撞,碰撞后两球交换速度.B球用长L的细线悬于O点,恰与水平地面切于D点.A球与水平地面间摩擦系数??=0.1,已知球A初始高度h=2m,CD=1m,g取10m/s2.问:
(1)若悬线L=2m,A与B能碰几次?最后A球停在何处?
(2)若球B能绕悬点O在竖直平面内旋转,L满足什么条件时,A、B将只能碰两次?A球最终停于何处?
(1)20次,停在C点 (2)L≤0.76m,最后停在C点右侧20m的地方
解析:
(1)由功能关系,![]() ①
① ![]() =20m ②
=20m ②
![]() =20 碰撞次数为20次
=20 碰撞次数为20次
最后球停在C点
(2)设刚好球B能做完整的圆周运动,并设其在最高点的速度为v1,在最低点的速度为v2
![]() ③
③
![]() ④
④
![]() ⑤
⑤
联立③④⑤并代入数据,得L≤0.76m
再由②式得最后停在C点右侧20m的地方。

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
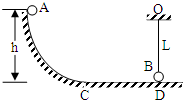 如图所示,球A无初速地沿光滑圆弧滑下至最低点C后,又沿水平轨道前进至D与质量、大小完全相同的球B发生动能没有损失的碰撞,碰撞后两球交换速度.B球用长L的细线悬于O点,恰与水平地面切于D点.A球与水平地面间摩擦系数μ=0.1,已知球A初始高度h=2m,CD=1m,g取10m/s2.问:
如图所示,球A无初速地沿光滑圆弧滑下至最低点C后,又沿水平轨道前进至D与质量、大小完全相同的球B发生动能没有损失的碰撞,碰撞后两球交换速度.B球用长L的细线悬于O点,恰与水平地面切于D点.A球与水平地面间摩擦系数μ=0.1,已知球A初始高度h=2m,CD=1m,g取10m/s2.问: