��Ŀ����
�˾۱�����뮡�밵�Ϊȼ�ϣ����а�ȫ���ྻ�������ḻ�����ŵ㣬�����ս��������ԴΣ��������Ч�ֶΣ�
��1������뮺�
H��ϳ�һ������
Heʱ��Ҫ�ų�ij�����ӣ�ͬʱ�ͷų�������д���˷�Ӧ�ķ��̣���뮺˵�����Ϊm1�����˵�����Ϊm2�����ų����ӵ�����Ϊm3��������˷�Ӧ���ͷų�������Ϊ���٣�
��2��Ҫʹ����뮺��ܹ������۱䷴Ӧ������ʹ�����Ծ���ٶȳ��ƿ��س���������һ����֪������뮺�ǡ���ܹ��˴˽Ӵ������۱�ʱ�����ǵĵ�����Ϊ
������eΪ뮺˵ĵ�����RΪ뮺˰뾶����0Ϊ��糣������Ϊ��֪��������������Զ������Ϊ������Ϊ�㣩�ĵ���뮺ˣ����پ��ж����ٶȲ����������˶�������һ��������۱䣿
��3������뮺˼��ȳɼ�����ȵĵ�����״̬ʱ�Ϳ���ʹ���������ٶȣ���һ���ôų�����Լ�������µ��������װ�ý������п����ˡ�����ͼ��ʾΪ�䡰Լ����ԭ��ͼ������ͬ��Բ�İ뾶�ֱ�Ϊr1��r2����������ֻ�ڰ뾶Ϊr1��Բ�������ڷ�Ӧ����Բ֮��Ļ������ڴ����Ŵ�ֱ�ڽ������ǿ�ų���Ϊ��֤����Ϊv��뮺˴ӷ�Ӧ������ų����ܴӴų��������߽���������Ӵų��Ÿ�Ӧǿ�ȵ���СֵΪ���٣����������ٶȴ�С��뮺�������Ӱ�죩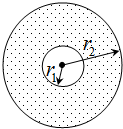
��1������뮺�
| 21 |
| 32 |
��2��Ҫʹ����뮺��ܹ������۱䷴Ӧ������ʹ�����Ծ���ٶȳ��ƿ��س���������һ����֪������뮺�ǡ���ܹ��˴˽Ӵ������۱�ʱ�����ǵĵ�����Ϊ
| e2 |
| 4����0(2R) |
��3������뮺˼��ȳɼ�����ȵĵ�����״̬ʱ�Ϳ���ʹ���������ٶȣ���һ���ôų�����Լ�������µ��������װ�ý������п����ˡ�����ͼ��ʾΪ�䡰Լ����ԭ��ͼ������ͬ��Բ�İ뾶�ֱ�Ϊr1��r2����������ֻ�ڰ뾶Ϊr1��Բ�������ڷ�Ӧ����Բ֮��Ļ������ڴ����Ŵ�ֱ�ڽ������ǿ�ų���Ϊ��֤����Ϊv��뮺˴ӷ�Ӧ������ų����ܴӴų��������߽���������Ӵų��Ÿ�Ӧǿ�ȵ���СֵΪ���٣����������ٶȴ�С��뮺�������Ӱ�죩

��1��
H��
He
n
��E=(2m1-m2-m3)c2
��2��һ��뮺˵Ķ���Ϊ��
m1
������
�������ٵ�뮺�������ײ��ǡ�ܷ����۱䣬�����ǵĶ��ܶ�ת��Ϊ������
2��
m1
=
�ɢۢܽ�� v1=
��3��뮺��ط�Ӧ�����߷�������ų���ƫת��ǡ������ų���߽����з��أ���Բ���˶��Ĺ켣�뾶��С��������ĴŸ�Ӧǿ����˴Ÿ�Ӧǿ�ȼ�Ϊ��֤����Ϊv��뮺��ز�ͬ����ӷ�Ӧ������ų����ܴӴų��������߽��������Сֵ��
���ݼ��ι�ϵ���У�r3=
����ţ�ٵڶ����ɣ��У�evB=m1
������ã�B=
�𣺣�1������˷�Ӧ���ͷų�������Ϊ(2m1-m2-m3)c2��
��2�����پ���
���ٶȲ����������˶�������һ��������۱䣻
��3�����Ӵų��Ÿ�Ӧǿ�ȵ���СֵΪ
��
| 2 | 21 |
| 32 |
| + | 01 |
��E=(2m1-m2-m3)c2
��2��һ��뮺˵Ķ���Ϊ��
| 1 |
| 2 |
| v | 21 |
�������ٵ�뮺�������ײ��ǡ�ܷ����۱䣬�����ǵĶ��ܶ�ת��Ϊ������
2��
| 1 |
| 2 |
| v | 21 |
| e2 |
| 4����0(2R) |
�ɢۢܽ�� v1=
| e |
| 2 |
|
��3��뮺��ط�Ӧ�����߷�������ų���ƫת��ǡ������ų���߽����з��أ���Բ���˶��Ĺ켣�뾶��С��������ĴŸ�Ӧǿ����˴Ÿ�Ӧǿ�ȼ�Ϊ��֤����Ϊv��뮺��ز�ͬ����ӷ�Ӧ������ų����ܴӴų��������߽��������Сֵ��
���ݼ��ι�ϵ���У�r3=
| r2-r1 |
| 2 |
����ţ�ٵڶ����ɣ��У�evB=m1
| v2 |
| r3 |
������ã�B=
| 2m1v |
| (r2-r1)e |
�𣺣�1������˷�Ӧ���ͷų�������Ϊ(2m1-m2-m3)c2��
��2�����پ���
| e |
| 2 |
|
��3�����Ӵų��Ÿ�Ӧǿ�ȵ���СֵΪ
| 2m1v |
| (r2-r1)e |

��ϰ��ϵ�д�
�����Ŀ
 ��2009?���ģ�⣩�˾۱�����뮡�밵�Ϊȼ�ϣ����а�ȫ���ྻ�������ḻ�����ŵ㣬�����ս��������ԴΣ��������Ч�ֶΣ�
��2009?���ģ�⣩�˾۱�����뮡�밵�Ϊȼ�ϣ����а�ȫ���ྻ�������ḻ�����ŵ㣬�����ս��������ԴΣ��������Ч�ֶΣ�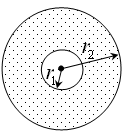
 ��ϳ�һ������
��ϳ�һ������ ʱ��Ҫ�ų�ij�����ӣ�ͬʱ�ͷų�������д���˷�Ӧ�ķ��̣���뮺˵�����Ϊm1�����˵�����Ϊm2�����ų����ӵ�����Ϊm3��������˷�Ӧ���ͷų�������Ϊ���٣�
ʱ��Ҫ�ų�ij�����ӣ�ͬʱ�ͷų�������д���˷�Ӧ�ķ��̣���뮺˵�����Ϊm1�����˵�����Ϊm2�����ų����ӵ�����Ϊm3��������˷�Ӧ���ͷų�������Ϊ���٣�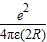 ������eΪ뮺˵ĵ�����RΪ뮺˰뾶����Ϊ��糣������Ϊ��֪��������������Զ������Ϊ������Ϊ�㣩�ĵ���뮺ˣ����پ��ж����ٶȲ����������˶�������һ��������۱䣿
������eΪ뮺˵ĵ�����RΪ뮺˰뾶����Ϊ��糣������Ϊ��֪��������������Զ������Ϊ������Ϊ�㣩�ĵ���뮺ˣ����پ��ж����ٶȲ����������˶�������һ��������۱䣿
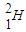 ��ϳ�һ������
��ϳ�һ������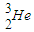 ʱ��Ҫ�ų�ij�����ӣ�ͬʱ�ͷų�������д���˷�Ӧ�ķ��̣���뮺˵�����Ϊm1�����˵�����Ϊm2�����ų����ӵ�����Ϊm3��������˷�Ӧ���ͷų�������Ϊ���٣�
ʱ��Ҫ�ų�ij�����ӣ�ͬʱ�ͷų�������д���˷�Ӧ�ķ��̣���뮺˵�����Ϊm1�����˵�����Ϊm2�����ų����ӵ�����Ϊm3��������˷�Ӧ���ͷų�������Ϊ���٣�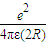 ������eΪ뮺˵ĵ�����RΪ뮺˰뾶����Ϊ��糣������Ϊ��֪��������������Զ������Ϊ������Ϊ�㣩�ĵ���뮺ˣ����پ��ж����ٶȲ����������˶�������һ��������۱䣿
������eΪ뮺˵ĵ�����RΪ뮺˰뾶����Ϊ��糣������Ϊ��֪��������������Զ������Ϊ������Ϊ�㣩�ĵ���뮺ˣ����پ��ж����ٶȲ����������˶�������һ��������۱䣿