题目内容
5. 一个面积为0.2m2的100匝线圈处在匀强磁场中,磁场方问垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R=6Ω,线圈电阻r=4Ω,求:
一个面积为0.2m2的100匝线圈处在匀强磁场中,磁场方问垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R=6Ω,线圈电阻r=4Ω,求:(1)线圈中磁通量的变化率和回路的感应电动势;
(2)a、b两点间电压Uab.
分析 根据磁感应强度的变化率求出磁通量的变化率,结合法拉第电磁感应定律求出回路中的感应电动势,通过欧姆定律求出ab两点间的电压.
解答 解:(1)磁通量的变化率$\frac{△Φ}{△t}$=$\frac{△B}{△t}$S=0.2×0.2=0.04Wb/s.
根据法拉第电磁感应定律得,感应电动势E=n$\frac{△Φ}{△t}$=100×0.04V=4V.
(2)根据欧姆定律得,ab间的电压U=$\frac{E}{{R}_{\;}+r}$R=$\frac{4}{6+4}$×6V=2.4V.
答:(1)磁通量变化率为0.04Wb/s;回路的感应电动势为4V;
(2)ab两点间电压Uab为2.4V.
点评 本题考查了法拉第电磁感应定律和闭合欧姆定律的基本运用,知道感应电动势E=n$\frac{△Φ}{△t}$=n$\frac{△B}{△t}$S的应用.

练习册系列答案
相关题目
13.关于做曲线运动的物体,以下说法正确的是( )
| A. | 速度一定是恒定不变的 | B. | 加速度一定是恒定不变的 | ||
| C. | 速率一定是恒定不变的 | D. | 受到的合外力一定不为零 |
20. 如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )
如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )
 如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )
如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )| A. | 逐渐增大 | B. | 先逐渐减小,后逐渐增大 | ||
| C. | 逐渐减小 | D. | 先逐渐增大,后逐渐减小 |
10.如果设行星的质量为m,绕太阳运动的线速度为v,公转周期为T,轨道半径为r,太阳的质量为M,则下列说法错误的是( )
| A. | 教材在探究太阳与行星的引力大小F的规律时,引入了公式F=m$\frac{{v}^{2}}{r}$,这个关系式实际上是牛顿第二定律 | |
| B. | 教材在探究太阳与行星的引力大小F的规律时,引入了公式v=$\frac{2πr}{T}$,这个这个关系式实际上是匀速圆周运动的一个公式 | |
| C. | 教材在探究太阳与行星间的引力大小F的规律时,引入了公式$\frac{{r}^{3}}{{T}^{2}}$=k,这个公式实质上是开普勒第三定律,是不可以在实验室中得到验证的 | |
| D. | 教材在探究太阳与行星间的引力大小F的规律时,得到的关系式F∝$\frac{m}{{r}^{2}}$之后,又借助相对运动的知识(即:也可理解为太阳绕行星做匀速圆周运动)得到F∝$\frac{M}{{r}^{2}}$,最终关系式用数学方法合并成F∝$\frac{Mm}{{r}^{2}}$ |
17.在太阳系中有一颗行星的半径为R,若在该星球表面以初速度V0竖直上抛出一物体,则该物体上升的最大高度为H.已知该物体所受的其他力与行星对它的万有引力相比较可忽略不计,万有引力常量为G.则根据这些条件,可以求出的物理量是( )
| A. | 该行星的自转周期 | B. | 该行星的密度 | ||
| C. | 该星球的第一宇宙速度 | D. | 绕该行星运行的卫星的最小周期 |
12.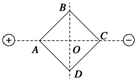 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )| A. | A点的电场强度等于B点的电场强度 | |
| B. | B、D两点的电场强度及电势均相同 | |
| C. | 一电子由B点沿B→C→D路径移至D点,电势能先减小后增大 | |
| D. | 一电子由C点沿C→O→A路径移至A点,电场力对其先做负功后做正功 |
 如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,试求:
如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,试求: 一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如图所示的交变电动势图象,试根据图象求出:
一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如图所示的交变电动势图象,试根据图象求出: