Question

（09年南昌市模拟）（12分）有一倾角为θ的斜面，其底端固定一档板，另有三个木块A、B、C，它们的质量分别为m_A = m_B = m，m_C = 3m，它们与斜面间的动摩擦因数都相同．其中木块A和一轻弹簧连接，放于斜面上，并通过轻弹簧与档板M相连，如图所示．开始时，木块A静止在P点弹簧处于原长，木块B在Q点以初速度U₀沿斜面向下运动，P、Q间的距离为l，已知木块B在下滑过程中做匀速直线运动，与木块A碰撞后立刻一起沿斜面向下运动，但不粘连，它们到达一个最低点后向上运动，木块B向上运动恰好能回到Q点．现将木块C从Q点以初速度沿斜面向下运动，木块A仍静止于P点，经历同样的过程，最后木块C停在斜面上的R点（图中未画出）．求：

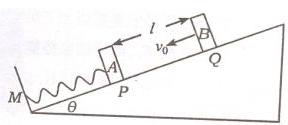
（1）A、B一起开始压缩弹簧时速度v₁；

       （2）A、B压缩弹簧的最大长度；

       （3）P、R间的距离l’的大小．

Answer 1

解析：（1）木块B下滑做匀速运动，有

 

             1分

 

    B和A碰撞后，设速度为，根据动量守恒定律得

 

            1分

 

    解得        1分

 

  （2）设两木块向下压缩弹簧的最大长度为x，两木块被弹簧弹回到P点时的速度为，根据动能定理得

 

          2分

 

    两木块在P点处分开后，木块B上滑到Q点的过程中，根据动能定理得

 

         1分

 

    解得           1分

 

（3）木块C与A碰撞前后速度为,根据动量守恒定律得

 

 

 

解得         1分

 

       设木块C与A压缩的最大长度为，两木块被弹簧弹回到P点时的速度为，根据动能定理得 

  

           1分

 

    木块C与A在P点处分开后，木块C上滑到R的过程中，根据动能定理得

 

      1分

 

在木块压缩弹簧的过程中，重力对木块所做的功与摩擦力对木块所做的功大小相等，因此，木块B和A压缩弹簧的初动能

 

 

木块C与A压缩弹簧的初动能即     1分

 

    因此，弹簧先后两次的最大压缩量相等，即，综上可得  1分