题目内容
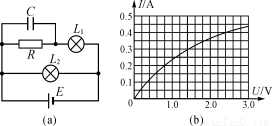
如图，用一根长为L＝1m的细线，一端系一质量为m＝1kg的小球（可视为质点），另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角θ＝37°，当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时，细线的张力为T。求（g＝10m/s2，sin370=3/5,cos370=4/5,计算结果可用根式表示）：
（1）若要小球离开锥面，则小球的角速度ω0至少为多大？
（2）若细线与竖直方向的夹角为60°，则小球的角速度ω＇为多大？
（3）细线的张力T与小球匀速转动的加速度ω有关，当ω的取值范围在0到ω＇之间时，请通过计算求解T与ω2的关系，并在坐标纸上作出T—ω2的图象，标明关键点的坐标值。
练习册系列答案
相关题目
倍，已知OA=AB，不计空气阻力，下列判断正确的是
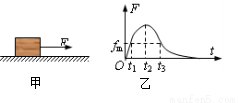
m的主动轮Q1和从动轮Q2及传送带等构成．两轮轴心相距8m，轮与传送带不打滑．现用此装置运送一袋面粉（可视为质点），已知这袋面粉与传送带之间的动摩擦因数为?＝0．4,这袋面粉中的面粉可不断地从袋中渗出．
、
两物体运动方向相反
时， 
、
两物体相遇
时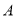
、
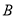两物体相距最远
、
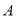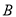两物体最远距离18m