题目内容
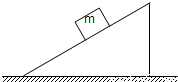
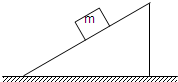 (1)一斜面体放在水平光滑的地面上,如图所示.斜面体高h=0.6m,底边长d=0.8m.一质量m=0.5kg的小滑块从斜面顶端由静止开始下滑.为了保持斜面体静止不动,需对斜面体施加一个水平向左大小为0.8N的推力F.求:
(1)一斜面体放在水平光滑的地面上,如图所示.斜面体高h=0.6m,底边长d=0.8m.一质量m=0.5kg的小滑块从斜面顶端由静止开始下滑.为了保持斜面体静止不动,需对斜面体施加一个水平向左大小为0.8N的推力F.求:①滑块与斜面之间的滑动摩擦因数μ.
②滑块从斜面顶端滑至底端经过的时间t.
(2)我国成功发射了“嫦娥一号”探测卫星,标志着中国航天正式开始了深空探测新时代.已知月球的半径约为地球的
| 1 |
| 4 |
| 1 |
| 6 |
分析:(1)先对小滑块受力分析,根据牛顿第二定律列式;再对斜面体受力分析,根据牛顿第二定律列式;最后联立求解即可;
(2)月球表面卫星周期最短,根据重力提供向心力列式求解即可.
(2)月球表面卫星周期最短,根据重力提供向心力列式求解即可.
解答:解:(1)①设物体与斜面间的摩擦因数为μ
物体在斜面下滑滑动摩擦力 f=μmgcosθ=4μ
斜面对物体的正压力 N=mgcosθ=4N
对斜面,在水平面 F+f cosθ-N sinθ=0
代入得 μ=0.5
②小滑块在斜面下滑的加速度为a,到斜面底端经历时间为t
由牛顿第二定律得 mg sinθ-μmgcosθ=ma
在斜面的运动过程 L=
at2
L=1m
代入得 t=1s
(2)绕月球飞行的卫星,轨道半径越小,则周期越短,因此周期最短的卫星在很靠近月球表面的轨道上运行,轨道半径可看成月球的半径.
设月球的半径为R月、月球表面的重力加速度为g月,卫星的最短周期为T,则
m(
)2R月=mg月 ①
将R月=
,g月=
g 代入可得
T=2π
②
代入数据解得卫星的最短周期约为
T=6×103s ③
答:(1)①滑块与斜面之间的滑动摩擦因数μ为0.5.
②滑块从斜面顶端滑至底端经过的时间t为1s.
(2)绕月球飞行的卫星的周期最短约为6×103s.
物体在斜面下滑滑动摩擦力 f=μmgcosθ=4μ
斜面对物体的正压力 N=mgcosθ=4N
对斜面,在水平面 F+f cosθ-N sinθ=0
代入得 μ=0.5
②小滑块在斜面下滑的加速度为a,到斜面底端经历时间为t
由牛顿第二定律得 mg sinθ-μmgcosθ=ma
在斜面的运动过程 L=
| 1 |
| 2 |
L=1m
代入得 t=1s
(2)绕月球飞行的卫星,轨道半径越小,则周期越短,因此周期最短的卫星在很靠近月球表面的轨道上运行,轨道半径可看成月球的半径.
设月球的半径为R月、月球表面的重力加速度为g月,卫星的最短周期为T,则
m(
| 2π |
| T |
将R月=
| R地 |
| 4 |
| 1 |
| 6 |
T=2π
|
代入数据解得卫星的最短周期约为
T=6×103s ③
答:(1)①滑块与斜面之间的滑动摩擦因数μ为0.5.
②滑块从斜面顶端滑至底端经过的时间t为1s.
(2)绕月球飞行的卫星的周期最短约为6×103s.
点评:第一小题关键分别对滑块和斜面体受力分析,然后根据牛顿第二定律和共点力平衡条件列方程求解;
第二小题关键根据重力等于向心力列式求解.
第二小题关键根据重力等于向心力列式求解.

练习册系列答案
相关题目
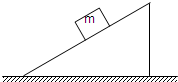 (1)一斜面体放在水平光滑的地面上,如图所示.斜面体高h=0.6m,底边长d=0.8m.一质量m=0.5kg的小滑块从斜面顶端由静止开始下滑.为了保持斜面体静止不动,需对斜面体施加一个水平向左大小为0.8N的推力F.求:
(1)一斜面体放在水平光滑的地面上,如图所示.斜面体高h=0.6m,底边长d=0.8m.一质量m=0.5kg的小滑块从斜面顶端由静止开始下滑.为了保持斜面体静止不动,需对斜面体施加一个水平向左大小为0.8N的推力F.求: ,月球表面的重力加速度约为地球的
,月球表面的重力加速度约为地球的 .地球半径R地=6.4×103km,地球表面的重力加速度g=9.8m/s2.求绕月球飞行的卫星的周期最短约为多少?(计算结果保留1位有效数字)
.地球半径R地=6.4×103km,地球表面的重力加速度g=9.8m/s2.求绕月球飞行的卫星的周期最短约为多少?(计算结果保留1位有效数字)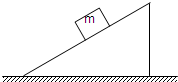
 ,月球表面的重力加速度约为地球的
,月球表面的重力加速度约为地球的 .地球半径R地=6.4×103km,地球表面的重力加速度g=9.8m/s2.求绕月球飞行的卫星的周期最短约为多少?(计算结果保留1位有效数字)
.地球半径R地=6.4×103km,地球表面的重力加速度g=9.8m/s2.求绕月球飞行的卫星的周期最短约为多少?(计算结果保留1位有效数字)