题目内容
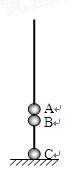
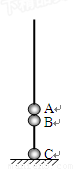
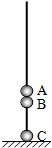 如图所示,三个都可以视为质点的小球A、B、C穿在竖直固定光滑绝缘细杆上,A、B紧靠在一起,C在绝缘地板上,它们的质量分别为mA=2.32kg,mB=0.20kg,mC=2.00kg,其中A不带电,B、C的带电荷量分别为qB=+4.0×10-5C,qC=+7.0×10-5C,且电荷量都保持不变.开始时,三个小球均静止.现在给A一个竖直向上的拉力F,使它开始做加速度为a=4.0m/s2的匀加速直线运动,经过时间t,拉力F变为恒力.(重力加速度g=10m/s2,静电引力常量k=9×109N?m2/c2)求:
如图所示,三个都可以视为质点的小球A、B、C穿在竖直固定光滑绝缘细杆上,A、B紧靠在一起,C在绝缘地板上,它们的质量分别为mA=2.32kg,mB=0.20kg,mC=2.00kg,其中A不带电,B、C的带电荷量分别为qB=+4.0×10-5C,qC=+7.0×10-5C,且电荷量都保持不变.开始时,三个小球均静止.现在给A一个竖直向上的拉力F,使它开始做加速度为a=4.0m/s2的匀加速直线运动,经过时间t,拉力F变为恒力.(重力加速度g=10m/s2,静电引力常量k=9×109N?m2/c2)求:(1)时间t;
(2)在时间t内,若B所受的电场力对B所做的功W=17.2J,则拉力F所做的功为多少.
分析:(1)研究开始静止状态,对AB整体,合力为零,由平衡条件和库仑定律求解开始时BC间的距离x1;给A施加力F后,AB沿斜面向上做匀加速运动,当AB分离之后F成为恒力,当两者之间弹力恰好为零时,根据牛顿第二定律得到BC距离,由运动学位移公式求出时间t;
(2)在时间t内,对AB运用动能定理求出电场力做功,即可求得拉力F所做的功.
(2)在时间t内,对AB运用动能定理求出电场力做功,即可求得拉力F所做的功.
解答:解:(1)开始时A、B处于平衡状态,设BC之间的距离为x1,则:
(MA+MB)g=k
,代入数据可得:x1=1.0m.
经时间t,F变为恒力.A、B恰好分离,A、B间无相互作用,设BC之间的距离为x2则:k
-MBg=MBa,
代入数据可得:x2=3.0m.
因为x2-x1=
at2,
代入数据可得:t=1s.
(2)以AB为系统,由动能定理可得:
WF+W电-(MA+MB)g(x2-x1)=
(MA+MB)v2
而v=at
代入数据可得:W拉=53.36J.
答:(1)时间t为1s;
(2)拉力F所做的功为53.36J.
(MA+MB)g=k
| qBqC | ||
|
经时间t,F变为恒力.A、B恰好分离,A、B间无相互作用,设BC之间的距离为x2则:k
| qBqC | ||
|
代入数据可得:x2=3.0m.
因为x2-x1=
| 1 |
| 2 |
代入数据可得:t=1s.
(2)以AB为系统,由动能定理可得:
WF+W电-(MA+MB)g(x2-x1)=
| 1 |
| 2 |
而v=at
代入数据可得:W拉=53.36J.
答:(1)时间t为1s;
(2)拉力F所做的功为53.36J.
点评:本题的解题关键是抓住AB刚分离时弹力为零,运用牛顿第二定律BC间的距离,要善于挖掘隐含的临界状态,把握临界条件进行分析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目