题目内容
质量为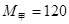 kg的甲船和质量为
kg的甲船和质量为 kg的乙船均静止于水面上,甲船上站着质量m=60 kg的人,通过一根长为L=12 m的绳用F=90 N的水平力拉乙船,求:
kg的乙船均静止于水面上,甲船上站着质量m=60 kg的人,通过一根长为L=12 m的绳用F=90 N的水平力拉乙船,求:
(1)两船相遇时,两船分别走了多少距离;
(2)当两船刚要相撞时,为防止两船相撞,人至少应以多大的水平速度(相对地面)由甲船跳上乙船.(忽略水的阻力)
(1)8m(2)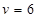 m/s
m/s
解析试题分析:(1)对甲船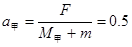 m/s2,
m/s2,
对乙船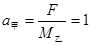 m/s2 ①
m/s2 ①
设人拉绳用了时间为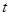 甲乙两船相遇,
甲乙两船相遇,
由位移关系得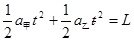 ②
②
解得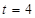 s
s
甲船位移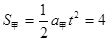 m,
m,
乙船位移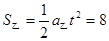 m,
m,
(2)设人相对地面以速度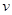 跳上乙船,取甲船的运动方向为正方向, 相遇前的瞬间:
跳上乙船,取甲船的运动方向为正方向, 相遇前的瞬间:
甲船的速率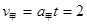 m/s(方向向右),
m/s(方向向右),
乙船的速率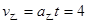 m/s(方向向左),
m/s(方向向左),
对甲船和人水平动量守恒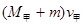 =
=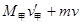 ③
③
对乙船和人水平动量守恒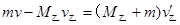 ④
④
为避免两船相撞的条件为: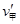 ≤
≤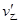 ⑤
⑤
联立③④⑤得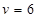 m/s
m/s
考点:匀变速直线运动、动量守恒定律
点评:本题考查了匀变速直线运动规律,通过动量守恒定律求物体的运动速度。在使用动量守恒定律时,应该先判断条件:系统合外力为零。

练习册系列答案
相关题目

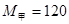 kg的甲船和质量为
kg的甲船和质量为 kg的乙船均静止于水面上,甲船上站着质量m=60 kg的人,通过一根长为L=12 m的绳用F=90 N的水平力拉乙船,求:
kg的乙船均静止于水面上,甲船上站着质量m=60 kg的人,通过一根长为L=12 m的绳用F=90 N的水平力拉乙船,求:
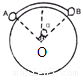
 kg的A球和质量为3kg的B球被轻绳连接后,挂在光滑的柱上恰好处于静止状态,已知∠AOB=90°,则OB与竖直方向的夹角α为( )
kg的A球和质量为3kg的B球被轻绳连接后,挂在光滑的柱上恰好处于静止状态,已知∠AOB=90°,则OB与竖直方向的夹角α为( )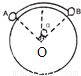
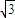 kg的A球和质量为3kg的B球被轻绳连接后,挂在光滑的柱上恰好处于静止状态,已知∠AOB=90°,则OB与竖直方向的夹角α为( )
kg的A球和质量为3kg的B球被轻绳连接后,挂在光滑的柱上恰好处于静止状态,已知∠AOB=90°,则OB与竖直方向的夹角α为( )