题目内容
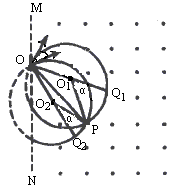
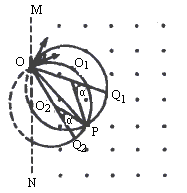
如下图中虚线MN是一垂直纸面的平面与纸面的交线,在平面右侧的半空间存在一磁感应强度为B、方向垂直纸面向外的匀强磁场.O是MN上的一点,从O点可以向磁场区域发射电荷量为+q、质量为m、速率为v的粒子,粒子射入磁场时的速度可在纸面内各个方向,已知先后射入的两个粒子恰好在磁场中给定的P点相遇,P到O的距离为L,不计重力和粒子间的相互作用.
(1)求所考察的粒子在磁场中的轨道半径.
(2)求这两个粒子从O点射入磁场的时间间隔.
答案:
解析:
解析:
|
(1)粒子在磁场中作圆周运动,向心力由洛伦兹力提供,其圆周轨道半径R=
(2)如图示,以OP为弦可画两个半径相同的圆,分别表示在P点相遇的两个粒子的轨道,圆心分别为O1和O2,在O处两个圆的切线分别表示两个粒子的射入方向,它们之间的夹角为α,由几何关系知 ∠PO1Q1=∠PO2Q2=α 从O点射入到相遇,粒子1的路程为半个圆周加弧长
t1= 粒子2运动时间
t2= 两粒子射入的时间间隔 Δt=t1-t2=2 由图知
R·cos 得 α=2arccos 故
Δt= |

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目