Question

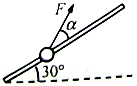如图，固定于竖直面内的粗糙斜杆，在水平方向夹角为30°，质量为m的小球套在杆上，在大小不变的拉力作用下，小球沿杆由底端匀速运动到顶端，为使拉力做功最小；
求（1）拉力F与杆的夹角a
（2）拉力F的大小．

Answer 1

解：解：∵小球匀速运动，由动能定理得；W_F+W_f-W_G=0
要使拉力做功最小则W_f=0，即摩擦力为0．
分析小球受的各力然后正交分解列方程：
垂直斜面方向：Fsinα=mgcos30°
沿斜面方向：Fcosα=mgsin30°
解以上两方程得：α=60°，F=mg
答：（1）拉力F与杆的夹角为60°；
（2）拉力F的大小为mg．
分析：要确定拉力做功最小的条件，要分析小球受到的各个力及做功情况：重力做负功，弹力不做功，拉力F做正功，又因小球做匀速运动，动能的变化为零，那么只要摩擦力不做功，即摩擦力为零，则拉力F做功最小，然后正交分解小球受到的各力，列力的平衡方程解答即可求出答案．
点评：解答本题的关键是通过分析小球的受力及各力做功情况，再结合动能定理得出拉力F做功最小时摩擦力为零．