题目内容
(15分)如图所示,质量为m的木板静止地放在光滑水平面上,质量为2m、可视为质点的木块以水平速度v0从左端滑上木板,木块与木板间的动摩擦因数为μ,木板足够长。
⑴求木块和木板的加速度大小;
⑵求木块和木板速度相等所经历的时间及此时木块相对于木板的位移;
⑶若木板不是足够长,要使木块不从木板上滑落,求木板的最小长度。
⑴a1=μg,a2=2μg;⑵t= ,Δs=
,Δs=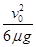 ;⑶Lmin=
;⑶Lmin=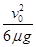
解析试题分析:⑴对木块,根据牛顿第二定律有:2μmg=2ma1,解得木块的加速度大小为:a1=μg
对木板,根据牛顿第二定律有:2μmg=ma2,解得木块的加速度大小为:a2=2μg
⑵设经时间t两者速度相等,且为v,此过程中木块的位移为s1,木板的位移为s2,根据匀变速直线运动速度公式有:v=v0-a1t=a2t,解得:t=
根据匀变速直线运动位移公式有:s1= ,s2=
,s2=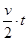
木块相对于木板的位移为:Δs=s1-s2,综合以上各式解得:Δs=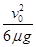
⑶由第⑵问的分析可知,当木板的长度L=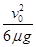 时,木块恰好滑至木板的最右端,两者具有了相同速度,往后将以此共同速度一起做匀速直线运动,所以木板的最小长度即为:Lmin=
时,木块恰好滑至木板的最右端,两者具有了相同速度,往后将以此共同速度一起做匀速直线运动,所以木板的最小长度即为:Lmin=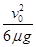
考点:本题主要考查了匀变速直线运动规律和牛顿运动定律的应用问题,属于中档题。

练习册系列答案
相关题目
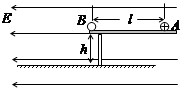
 水平抛出,与此同时,在A的正下方有一物块B也以相同的初速度
水平抛出,与此同时,在A的正下方有一物块B也以相同的初速度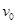 同方向滑出,B与地面间的动摩擦因数为
同方向滑出,B与地面间的动摩擦因数为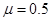 ,A、B均可看做质点,空气阻力不计。求:
,A、B均可看做质点,空气阻力不计。求:
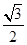 ,取g=10 m/s2。
,取g=10 m/s2。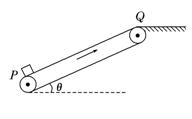

 =0.3,当车运行了1.5 s时,被地面装置锁定(g=10m/s2)。求:
=0.3,当车运行了1.5 s时,被地面装置锁定(g=10m/s2)。求: