题目内容
一列横波在x轴线上传播着,在t1=0和t2=0.04s时的波形曲线分别如图所示:
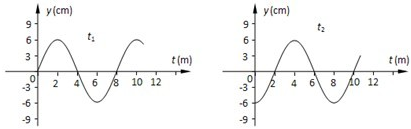
①读出简谐波的波长是
②设周期大于(t2-t1).如果波向右传播,波速多大?
③若波速的大小为2750m/s,求波的传播方向.

①读出简谐波的波长是
8
8
m;振幅是0.06
0.06
m.②设周期大于(t2-t1).如果波向右传播,波速多大?
③若波速的大小为2750m/s,求波的传播方向.
分析:(1)由波动图象读出波长和振幅.振幅等于质点振动位移的最大值.
(2)若周期大于(t2-t1),即传播时间(t2-t1)小于T,波传播的距离小于一个波长,即得到波传播的距离x,由v=
求得波速.
(3)已知波速,由x=vt求出(t2-t1)时间传播的距离,根据波形的平移法确定波的传播方向.
(2)若周期大于(t2-t1),即传播时间(t2-t1)小于T,波传播的距离小于一个波长,即得到波传播的距离x,由v=
| x |
| t |
(3)已知波速,由x=vt求出(t2-t1)时间传播的距离,根据波形的平移法确定波的传播方向.
解答:解:(1)由图知,波长λ=8m,振幅A=6cm=0.06m
(2)若波向右传播,因周期大于(t2-t1),即传播时间(t2-t1)小于T,波传播的距离小于一个波长,则得到波传播的距离x=2m
所以波速v=
=
=
m/s=50m/s
(3)若v=2750m/s,则波在(t2-t1)时间传播的距离x=vt=2750×0.04m=110m=13
λ,相当于
λ,由波形的平移法得知,波向左传播.
故答案为:
(1)8m;0.06m
(2)50m/s
(3)向左传播.
(2)若波向右传播,因周期大于(t2-t1),即传播时间(t2-t1)小于T,波传播的距离小于一个波长,则得到波传播的距离x=2m
所以波速v=
| x |
| t |
| x |
| t2-t1 |
| 2 |
| 0.04 |
(3)若v=2750m/s,则波在(t2-t1)时间传播的距离x=vt=2750×0.04m=110m=13
| 3 |
| 4 |
| 3 |
| 4 |
故答案为:
(1)8m;0.06m
(2)50m/s
(3)向左传播.
点评:本题关键要抓住波的周期性和双向性,根据波形的平移法确定波传播距离与波长的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
