题目内容
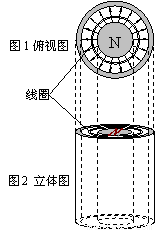
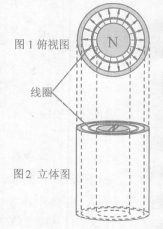
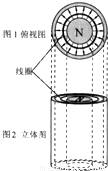
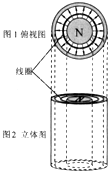 一个足够长的竖直放置的磁铁结构如图所示.在图1中磁铁的两个磁极分别为同心的圆形和圆环形.在两极之间的缝隙中,存在辐射状的磁场,磁场方向水平向外,某点的磁感应强度大小与该点到磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度被无初速释放,在磁极缝隙间下落的过程中,线圈平面始终水平且保持与磁极共轴.线圈被释放后( )
一个足够长的竖直放置的磁铁结构如图所示.在图1中磁铁的两个磁极分别为同心的圆形和圆环形.在两极之间的缝隙中,存在辐射状的磁场,磁场方向水平向外,某点的磁感应强度大小与该点到磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度被无初速释放,在磁极缝隙间下落的过程中,线圈平面始终水平且保持与磁极共轴.线圈被释放后( )分析:由于线圈切割磁感线,则线圈中会产生感应电流,由右手定则可得出线圈中的电流方向;根据线圈的运动过程可知线圈能达的最大速度,并能得出其表达式;由题意结合表达式可得出线圈半径与最大速度间的关系.
解答:解:因线圈在下落过程中切割磁感线,故线圈中会产生感应电流;在任意一点由右手定则可知电流方向应为顺时针;故AB错误;
线圈在磁场中做向下的变加速直线运动,速度越大,电流越大,安培力越大;则安培力等于重力时,线圈将做匀速直线运动;
则有BIL=
=mg;
R=ρ
则有:
=ρ1SLg;
解得:v=
若线圈半径越大,则切割处的磁感应强度越小,由公式可得最大速度越大;
故选D.
线圈在磁场中做向下的变加速直线运动,速度越大,电流越大,安培力越大;则安培力等于重力时,线圈将做匀速直线运动;
则有BIL=
| B2L2V |
| R |
R=ρ
| L |
| s |
则有:
| B2LVS |
| ρ |
解得:v=
| ρ1ρg |
| B2 |
若线圈半径越大,则切割处的磁感应强度越小,由公式可得最大速度越大;
故选D.
点评:本题中要注意圆形线圈在圆形磁场中运动,故可以认为是直导线切割磁感线;注意导线的电阻和质量均与导线的长度有关,应分别根据密度公式和电阻定律列出表达式再推出最后的公式,即可明确最大速度.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目