题目内容
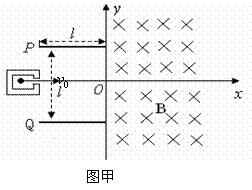
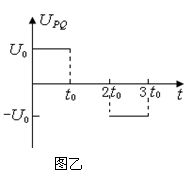
(17分) 如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴间右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子在0~3t0时间内两板间加上如图乙所示的电压(不考虑极边缘的影响)。
已知t=0时刻进入两板间的带电粒子恰好在t0时,刻经极板边缘射入磁场。上述m、q、![]() 、t0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)
、t0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)
(1)求电压U0的大小。
(2)求t0时刻进入两板间的带电粒子在磁场中做圆周运动的半径。
(3)带电粒子在磁场中的运动时间。
 |
 |
(17分)
解:(1)t=0时刻进入两极板的带电粒子在电场中做匀变速曲线运动,t0时刻刚好从极板边缘射出,在y轴负方向偏移的距离为l/2,则有
![]() (1分)
(1分)
Eq=ma (1分)
l/2=at02/2 (1分)
联立解得两极板间偏转电压为![]() 。(2分)
。(2分)
(2)t0时刻进入两极板的带电粒子,两极板没有电场,带电粒子做匀速直线运动。
带电粒子沿x轴方向的分速度大小为v0=l/t0 (2分)
设带电粒子离开电场进入磁场做匀速圆周运动的半径为R,则有![]() (1分)
(1分)
联立⑤⑥式解得![]() (1分)。
(1分)。
(3)2t0时刻进入两极板的带电粒子在磁场中运动时间最短。带电粒子离开磁场时沿y轴正方向的分速度为vy=at0,
设带电粒子离开电场时速度方向与y轴正方向的夹角为![]() ,则
,则![]() ,(2分)
,(2分)
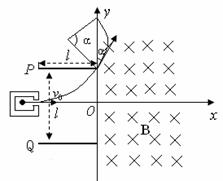
联立解得![]() ,带电粒子在磁场运动的轨迹图如图所示,圆弧所对的圆心角为
,带电粒子在磁场运动的轨迹图如图所示,圆弧所对的圆心角为![]() ,所求最短时间为
,所求最短时间为![]() , (1分)
, (1分)
带电粒子在磁场中运动的周期为![]() ,联立以上两式解得
,联立以上两式解得![]() 。(2分)
。(2分)
同理,t=0进入两极板的带电粒子在磁场中运动的时间最长为:![]() (2分)
(2分)
所以,带电粒子在磁场中的运动时间:![]() (1分)
(1分)


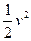 和
和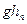 的值。验证机械能守恒定律
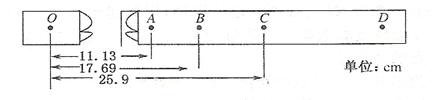
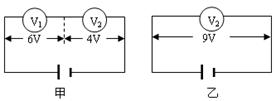
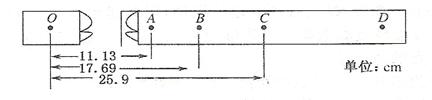
的值。验证机械能守恒定律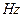 的交流电,用最小刻度为1mm的刻度尺,测得OA=11.13m,OB=17.69m,OC=25.9m.这三个数据中不符合有效数据要求的是___,在计数点A和B之间,B和C之间各还有一个点,重锤的质量为
的交流电,用最小刻度为1mm的刻度尺,测得OA=11.13m,OB=17.69m,OC=25.9m.这三个数据中不符合有效数据要求的是___,在计数点A和B之间,B和C之间各还有一个点,重锤的质量为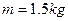 ,根据以上数据,当打点到B点时重锤的重力势能比开始下落时减少了___,这时它的动能是__.(
,根据以上数据,当打点到B点时重锤的重力势能比开始下落时减少了___,这时它的动能是__.(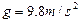 )
)
 。
。
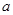 = (用字母表示)
= (用字母表示) 图线,如图丙中的实线所示.试分析:图线不通过坐标原点O的原因是
,曲线上部弯曲的原因是
17.(10分)某兴趣小组为了测量一待测电阻
图线,如图丙中的实线所示.试分析:图线不通过坐标原点O的原因是
,曲线上部弯曲的原因是
17.(10分)某兴趣小组为了测量一待测电阻 的阻值,准备先用多用电表粗测出它的阻值,然后再用伏安法精确地测量.实验中准备了以下器材:
的阻值,准备先用多用电表粗测出它的阻值,然后再用伏安法精确地测量.实验中准备了以下器材: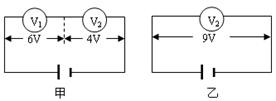
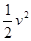 和
和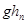 的值。验证机械能守恒定律
的值。验证机械能守恒定律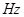 的交流电,用最小刻度为1mm的刻度尺,测得OA=11.13m,OB=17.69m,OC=25.9m.这三个数据中不符合有效数据要求的是___,在计数点A和B之间,B和C之间各还有一个点,重锤的质量为
的交流电,用最小刻度为1mm的刻度尺,测得OA=11.13m,OB=17.69m,OC=25.9m.这三个数据中不符合有效数据要求的是___,在计数点A和B之间,B和C之间各还有一个点,重锤的质量为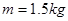 ,根据以上数据,当打点到B点时重锤的重力势能比开始下落时减少了___,这时它的动能是__.(
,根据以上数据,当打点到B点时重锤的重力势能比开始下落时减少了___,这时它的动能是__.(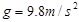 )
)