题目内容
 光滑的
光滑的| 1 |
| 4 |
. |
| DE |
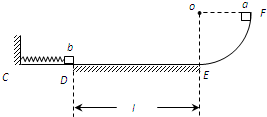
(1)物块a第一次经过E点时的速度是多少?
(2)试讨论l取何值时,a、b能且只能发生一次碰撞?
分析:(1)根据机械能守恒定律求出物块a第一次经过E点时的速度.
(2)根据动能定理和动量守恒定律求出a、b一起压缩弹簧时的速度,根据物块a到达D点的速度不为零,求出l的范围,以及知道a、b只发生一次碰撞,物块a滑上圆弧轨道又返回,最终停在水平轨道上P点,物块b在水平轨道上匀减速滑至P点也恰好停止.结合动能定理求出l的范围.
(2)根据动能定理和动量守恒定律求出a、b一起压缩弹簧时的速度,根据物块a到达D点的速度不为零,求出l的范围,以及知道a、b只发生一次碰撞,物块a滑上圆弧轨道又返回,最终停在水平轨道上P点,物块b在水平轨道上匀减速滑至P点也恰好停止.结合动能定理求出l的范围.
解答:解:(1)物块a由F到E过程中,由机械能守恒有:mgr=
m
解得第一次经过E点时的速度 v1=
(2)物块a从E滑至D过程中,由动能定理有:-μ1mgl=
m
-
m
解得物块a在D点时的速度 vD1=
)
物块a、b在D点碰撞,根据动量守恒有:mvD1=3mvD2
解得两物块在D点向左运动的速度vD2=
a、b一起压缩弹簧后又返回D点时速度大小vD3=
由于物块b的加速度大于物块a的加速度,所以经过D后,a、b两物块分离,同
时也与弹簧分离.
讨论:①假设a在D点时的速度vD1=0,即 l=5r
要使a、b能够发生碰撞,则l<5r
②假设物块a滑上圆弧轨道又返回,最终停在水平轨道上P点,物块b在水平轨道上匀减速
滑至P点也恰好停止,设
=x,则
=l-x,根据能量守恒,
对a物块 μ1mg(l+x)=
m
对b物块 μ22mg(l-x)=
2m
由以上两式解得 x=
l
将x=
l代入 μ1mg(l+x)=
m
解得 l=
r
要使a、b只发生一次碰撞,则l≥
r
综上所述,当5r>l≥
r时,a、b两物块能且只能发生一次碰撞.
答:(1)物块a第一次经过E点时的速度是v1=
.
(2)当5r>l≥
r时,a、b两物块能且只能发生一次碰撞.
| 1 |
| 2 |
| v | 2 1 |
解得第一次经过E点时的速度 v1=
| 2gr |
(2)物块a从E滑至D过程中,由动能定理有:-μ1mgl=
| 1 |
| 2 |
| v | 2 D1 |
| 1 |
| 2 |
| v | 2 1 |
解得物块a在D点时的速度 vD1=
| 2g(r-0.2l |
物块a、b在D点碰撞,根据动量守恒有:mvD1=3mvD2
解得两物块在D点向左运动的速度vD2=
| ||
| 3 |
a、b一起压缩弹簧后又返回D点时速度大小vD3=
| ||
| 3 |
由于物块b的加速度大于物块a的加速度,所以经过D后,a、b两物块分离,同
时也与弹簧分离.
讨论:①假设a在D点时的速度vD1=0,即 l=5r
要使a、b能够发生碰撞,则l<5r
②假设物块a滑上圆弧轨道又返回,最终停在水平轨道上P点,物块b在水平轨道上匀减速
滑至P点也恰好停止,设
. |
| PE |
. |
| DP |
对a物块 μ1mg(l+x)=
| 1 |
| 2 |
| v | 2 D3 |
对b物块 μ22mg(l-x)=
| 1 |
| 2 |
| v | 2 D3 |
由以上两式解得 x=
| 1 |
| 3 |
将x=
| 1 |
| 3 |
| 1 |
| 2 |
| v | 2 D3 |
解得 l=
| 5 |
| 13 |
要使a、b只发生一次碰撞,则l≥
| 5 |
| 13 |
综上所述,当5r>l≥
| 5 |
| 13 |
答:(1)物块a第一次经过E点时的速度是v1=
| 2gr |
(2)当5r>l≥
| 5 |
| 13 |
点评:本题综合考查了机械能守恒定律、动量守恒定律和动能定理,对学生能力的要求较高,对于a、b能且只能发生一次碰撞,找出临界状况是解决本题的关键,对学生而言是一难点.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图所示,水平轨道PAB与
如图所示,水平轨道PAB与