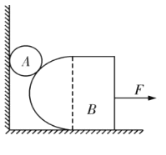
题目内容
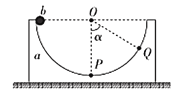
【题目】如图所示,光滑水平面放置一个静止的质量为2m的带有半圆形轨道的滑块a,半圆形轨道的半径为R。一个质量为m的小球b从半圆轨道的左侧最高点处由静止释放,b到达半圆轨道最低点P时速度大小![]() ,然后进入右侧最高可到点Q,OQ连线与OP间的夹角
,然后进入右侧最高可到点Q,OQ连线与OP间的夹角![]() =
=![]() ,不计空气阻力,重力加速度为g。下列说法正确的是( )
,不计空气阻力,重力加速度为g。下列说法正确的是( )
A.滑块a向左滑行的最大距离为0.6R
B.小球b从释放到滑到Q点的过程中,克服摩擦力做的功为0.4mgR
C.小球b第一次到达P点时对轨道的压力为1.8mg
D.小球b第一次返回到P点时的速度大于![]()
【答案】AD
【解析】
A.滑块a和小球b相互作用的过程,系统水平方向合外力为零,系统水平方向动量守恒,小球b到达Q点时,根据动量守恒定律得滑块a和小球b的速度均为零,有
2msa=msb
sa+sb=R+Rsin![]()
解得
sa=0.6R
故A正确;
B.根据功能关系得小球b从释放到滑到Q点的过程中,克服摩擦力做的功为
![]()
故B错误;
C.当b第一次到达半圆轨道最低点P时,根据动量守恒定律有
2mva=mvb
解得
![]()
由牛顿运动定律得
![]()
解得
![]()
对轨道的压力
![]()
故C错误;
D.小球从P点到Q点,根据功能关系可得克服摩擦力做的功为
![]()
由功能关系结合圆周运动的知识,得小球b第一次返回到P点的过程中克服摩擦力做的功
W′<0.2mgR
故小球b第一次返回到P点时系统的总动能
![]()
![]()
![]()
解得
![]()
故D正确。
故选AD。

练习册系列答案
相关题目