��Ŀ����
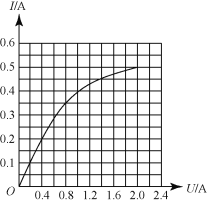
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxOy��ƽ���ڣ���һ���뾶ΪR��Բ��O1����Ϊ��0����3R����Բ�����������ڴ����ŴŸ�Ӧǿ��ΪB1������ֱ����ƽ���������ǿ�ų�����һ��ƽ�е缫�崹ֱ��x���ҹ���y��ԳƷ��ã�����AB��CD�ij��Ⱥ��������Ϊ2R������������˵�B��Dλ��x���ϣ�AB������磬CD������硣�ڵ�һ�͵ڶ������ڣ�����x�����y���ϣ��д�ֱ������ƽ������ĴŸ�Ӧǿ��ΪB2��δ��֪������ǿ�ų�������һ�鳤ΪR��Ȳ��Ƶ��ռ���EFλ��x����2R��3R�������ϡ�����һ�����ڣ�R����3R���ĵ���Դ��������ƽ������Բ������ų����������Ϸ������ʾ�Ϊ![]() ��������y��������н�Ϊ�ȣ�������0��180���ڱ仯���ĵ��ӡ���֪���ӵĵ������СΪe������Ϊm�����Ƶ����������ã����Ƶ���֮������������������֮��ĵ糡������ǿ�糡�Һ��Լ���ı�ԵЧӦ������������AB�������̱������Ҳ��ı�ԭ�糡�ֲ����������ܾ�����һ�������Ĵų�������ռ�����Ҳ���̱����գ��������ռ���Ĵ��ڶԵ����˶���Ӱ�죩��������û�д����ռ��������Ǻ������˶�����
��������y��������н�Ϊ�ȣ�������0��180���ڱ仯���ĵ��ӡ���֪���ӵĵ������СΪe������Ϊm�����Ƶ����������ã����Ƶ���֮������������������֮��ĵ糡������ǿ�糡�Һ��Լ���ı�ԵЧӦ������������AB�������̱������Ҳ��ı�ԭ�糡�ֲ����������ܾ�����һ�������Ĵų�������ռ�����Ҳ���̱����գ��������ռ���Ĵ��ڶԵ����˶���Ӱ�죩��������û�д����ռ��������Ǻ������˶�����
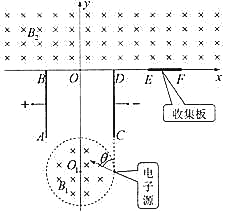
��1��������=60������ĵ����ܹ�����ԭ��O������������ѹΪ���
��2��Ҫʹ�ڣ�1�����еĵ����ܱ��ռ������գ���B2ӦΪ���
��3����B2=B1���������ĵ�ѹΪ�ڣ�1�����еĵ�ѹ��Ҫʹ�ռ�����Ҷ˵�F�����ӻ��У����ռ�������˵�E��ʱ����ת�ĽǶ����ٶ���𰸿��÷����Ǻ�����ʾ������cos��=![]() �������ɱ�ʾΪarccos
�������ɱ�ʾΪarccos![]() ��
��
��4����B2=![]() B1���������ĵ�ѹ��С���Դ�0��ʼ���ڣ������弫�Բ��䣩�������Щ�Ƕȷ���ĵ��ӿɻ����ռ�����Ҷ˵�F��
B1���������ĵ�ѹ��С���Դ�0��ʼ���ڣ������弫�Բ��䣩�������Щ�Ƕȷ���ĵ��ӿɻ����ռ�����Ҷ˵�F��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4���ȡ�120������ĵ��ӿɻ����ռ�����Ҷ˵�F
����4���ȡ�120������ĵ��ӿɻ����ռ�����Ҷ˵�F
��������
�������������������������Բ�δų�����Ĺ���뾶�������ɼ��ι�ϵ��ý���糡��λ�ú��ٶȷ����ٸ����ȱ����˶�������ü��ٶȣ����ɵõ���ѹ�����ݵ���������Բ���˶����ɼ��ι�ϵ��ù���뾶��Χ�����ɸ���������������������ôŸ�Ӧǿ�ȷ�Χ�����������˶��õ���ת�Ƕ���Сʱ��Ӧ�������Ȼ����ݼ��ι�ϵ��⣻�ɼ��ι�ϵ��ò�ͬλ�ý���y��0����ĵ��ӵĹ���뾶��Ȼ����������������������õ��ٶȷ�Χ�����ɸ��ݵ��ӵ���ֱ���ٶȲ���õ���Χ���Ӷ��õ��Ƕȷ�Χ��
��1��������Բ�Ĵų�������������Բ���˶����ٶ�![]()
����������������������![]()
��ù���뾶��![]()
���ݼ��ι�ϵ�ɵã������뿪Բ�Ĵų�ʱ���ٶȷ�����ֱ���ϣ���ô�������˶���O��Ĺ켣��ͼ��ʾ��
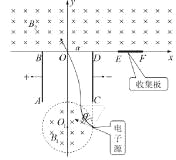
�����ڼ�����˶�ֻ�ܵ糡�����ã��ʵ�������ƽ���˶������ٶ�![]()
��ֱλ��Ϊ2R��ˮƽλ��Ϊ![]()
����2R=v0t��![]()
������������ѹ��![]()
��2���ɣ�1���ɵã�������O��ʱ��ˮƽ���ٶ�![]()
���������y��0����������Բ���˶��Ĺ���뾶ΪR2�����ɼ��ι�ϵ�ɵã������ٴξ���x�������![]()
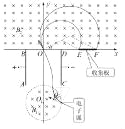
�ʸ����ռ���λ�ã�Ҫʹ�ڣ�1�����еĵ����ܱ��ռ������գ����У�![]() ��
��
�ٸ��������������������ɵã�![]() �����ԣ�����뾶
�����ԣ�����뾶![]() ���ų�ǿ��
���ų�ǿ��![]() ��
��
���ԣ�![]() ������
������![]() �����ԣ�
�����ԣ�![]()
��3����B2=B1���������y��0����������Բ���˶��Ĺ���뾶Ϊ![]()
����=0����ĵ��Ӵ����ռ����Ҷ˵�Fʱ���ռ�������˵�E��ʱ����ת�ĽǶ�����С����ʱ�����ӽ���y��0����ʱ���ٶȷ�����x���ļн�![]() ����x���ϵ�����
����x���ϵ�����![]()
���ʱF������Ϊ��X��Y�������ɼ��ι�ϵ�ɵã�![]() ����X��2R��2+Y2=R2��
����X��2R��2+Y2=R2��![]() ��
��
���ԣ�![]() ��
��![]() ��
�� ![]() ��
��
��4������ӽ���y��0����ʱ���ٶ�Ϊv����F�ľ���Ϊ2d������������Բ���˶��Ĺ���뾶Ϊr������ֱ����Ϊv0��
�ɼ��ι�ϵ�ɵã�![]()
���������������������ɵã�![]() �����ԣ�
�����ԣ�![]() ����
����![]() ��
��
�ʴ�![]() ���뿪�糡�ĵ��ӿ��Ի����ռ�����Ҷ˵�F��
���뿪�糡�ĵ��ӿ��Ի����ռ�����Ҷ˵�F��
�����������ĵ�ѹ��С���Դ�0��ʼ���ڣ����ӽ���糡ʱ���ٶ���ֱ���ϣ��ڵ糡���˶�����ƫת�����ԣ��뿪Բ�δų�����ʱ��x��������![]() ��Χ�ڵĵ�����Ի����ռ�����Ҷ˵�F�����ݵ�����Բ�δų�����Ĺ���뾶ΪR���ɼ��ι�ϵ�ɵã�����120�㣻
��Χ�ڵĵ�����Ի����ռ�����Ҷ˵�F�����ݵ�����Բ�δų�����Ĺ���뾶ΪR���ɼ��ι�ϵ�ɵã�����120�㣻

 ѧϰʵ����ϵ�д�
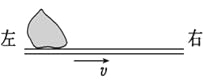
ѧϰʵ����ϵ�д�����Ŀ��ijͬѧ��̽��С���ٶ���ʱ��仯�Ĺ���ʱ���Դ����һ��ֽ�������о�����O�㿪ʼÿ5�������Ϊһ�������㣨�м�4�����δ��������ԴƵ��Ϊ50���ȣ���������ֱ�ΪA��B��C��D��E����ͬѧ��������������Ӧ���ٶȣ�����ֵ���±��������������λ��Ч���֣�

������ | A | B | C | D | E |
�ٶ�/�� | 0.70 | 0.91 | 1.10 | 1.30 | 1.49 |
��1��������������������������ֽ������С����![]() ͼ�ߣ�������O��Ϊ��ʱ��㣬�ʵ�����ᡢ������̶ȣ���
ͼ�ߣ�������O��Ϊ��ʱ��㣬�ʵ�����ᡢ������̶ȣ���
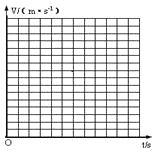
��2��������O��Ӧ���ٶ�Ϊ m/s�����ٶ�Ϊ m/s2��������3λ��Ч���֣�