题目内容
如图(a),磁铁A、B的同名磁极相对放置,置于水平气垫导轨上。A固定于导轨左端,B的质量m=0.5kg,可在导轨上无摩擦滑动。将B在A附近某一位置由静止释放,由于能量守恒,可通过测量B在不同位置处的速度,得到B的势能随位置x的变化规律,见图(c)中曲线I。若将导轨右端抬高,使其与水平桌面成一定角度θ[如图(b)所示],则B的总势能曲线如图(c)中II所示(设B在x=0处时重力势能为零)。在图(b)的情况下,若将B放在x=15.0cm处,则B在该位置时的重力势能为________J, 气垫导轨的倾角θ为________;若将B在x=15.0cm处静止释放,则它能达到的最大速度为________ m/s,此时B受到的磁场力为________ N。(计算时取g=10m/s2)

0.60(2分),53.1°(2分),0.85(±0.01)(2分),4.0(2分)
分析:根据曲线I读出在x=15.0cm处的势能是0.1J,根据曲线II读出在x=15.0cm处的总势能是0.7J,运用能量守恒求出B在该位置时的重力势.
根据重力势能的定义求出倾角θ.
根据功能关系可知,当势能最小时,动能最大.由图得出释放时的势能便是整个运动过程中的总能量,根据能量转化与守恒可知势能最小时动能最大,据此可求得最大速度.
解:根据曲线I读出在x=15.0cm处的势能是0.1J,根据曲线II读出在x=15.0cm处的总势能是0.7J,
运用能量守恒得
x=15.0cm处,则B在该位置时的重力势能为0.7J-0.1J=0.6J
根据重力势能的定义Ep=mgh
所以h=0.12m
所以sinθ=
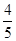 ,即θ=53.1°
,即θ=53.1°由图读得释放处(x=15.0cm处)势能Ep=0.70J,此即B的总能量.由于运动中总能量守恒,
因此在势能最小处动能最大,由图象得最小势能为0.5J,
则最大动能为Ekm=0.7-0.52=0.18J
最大速度为vm=
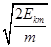 =0.85(m/s)
=0.85(m/s)最大速度位置B的加速度为零,所以B受到的磁场力为mgsinθ=4.0N.
故答案为:0.6,53.1°,0.85(±0.01),4.0.

练习册系列答案
相关题目


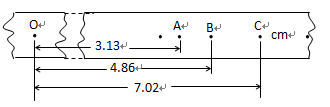
 = m/s,
= m/s,
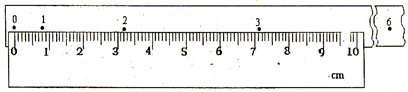
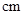 ,计数点3对应的刻度尺的读数为
,计数点3对应的刻度尺的读数为 

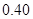

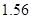


 图象;
图象; 。
。