题目内容
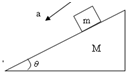如图，质量为M的斜面体斜面倾角为θ，质量为m的物体以加速度a沿斜面加速下滑，斜面体不动，则水平面对斜面体的支持力是（ ）分析：物体以加速度a加速下滑，加速度方向沿斜面向下，以B和斜面体A整体作为研究对象，分析受力情况，将物体的加速度分解为水平和竖直两个方向，根据牛顿第二定律分析和求解地面对斜面体的支持力．
解答：解：将物体的加速度a分解为水平和竖直两个方向，如图：
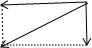
以整体为研究对象，在竖直方向上，则有（M+m）g-N=masinθ，
则N=（M+m）g-masinθ．
故选：B．
以整体为研究对象，在竖直方向上，则有（M+m）g-N=masinθ，
则N=（M+m）g-masinθ．
故选：B．
点评：运用牛顿第二定律运用整体法研究，技巧是将加速度分解，而不分解力，简单方便．
练习册系列答案
相关题目
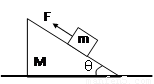
如图，质量为M的斜面放在粗糙的水平地面上．几个质量都是m的不同物块，先后在斜面上以不同的加速度向下滑动，斜面始终保持静止不动．下列关于水平地面对斜面底部的支持力和静摩擦力的几种说法中不正确的有（ ）| A、匀速下滑时，支持力N=（m+M）g，静摩擦力为零 | B、匀加速下滑时，支持力N＜=（m+M）g静摩擦力的方向水平向左 | C、匀减速下滑时，支持力N＞=（m+M）g静摩擦力的方向水平向右 | D、无论怎样下滑，总是N=（m+M）g静摩擦力为零 |
静摩擦力为零；
静摩擦力的方向水平向右；
静摩擦力的方向水平向右；
静摩擦力为零；
静摩擦力的方向水平向右；