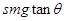题目内容
如图4所示，质量为M的木板放在倾角为θ的光滑斜面上，质量为m的人在木板上跑，假如脚与板接触处不打滑.
（1）要保持木板相对斜面静止，人应以多大的加速度朝什么方向跑动？
（2）要保持人相对于斜面的位置不变，人在原地跑而使木板以多大的加速度朝什么方向运动？
人或板运动的加速度都是沿斜面方向的，脚与板不打滑，产生的静摩擦力，也是沿斜面方向的.一个静止，另一个沿斜面做加速运动，都是沿斜面方向的合力作用的结果，因此只要建立沿斜面方向的一个坐标即可.
（1）对木板，沿坐标x轴的受力和运动情况如图5所示，木板视为质点，由牛顿第二定律可得
Mgsinθ-f1=0
对人，由牛顿第三定律知f1′与f1等大反向，所以沿x正方向受mgsinθ和f1′的作用.由牛顿第二定律可得 f1′+mgsinθ=ma
由以上二方程联立求解得a=
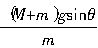，方向沿斜面向下.（2）对人，沿x轴方向受力和运动情况如图6所示 .视人为质点，根据牛顿第二定律得 mgsinθ-f2=0.
对木板，由牛顿第三定律知f2′和f2等值反向，所以木板沿x正方向受Mgsinθ和f2′的作用.根据牛顿第二定律得f2′+Mgsinθ=Ma
由上述二式解得a=
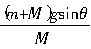，方向沿斜面向下.【试题分析】
练习册系列答案
阅读快车系列答案
相关题目
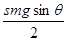
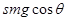D．