题目内容
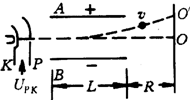 如图所示电子射线管阴极K发射电子,阳极P和阴极K间加上电压后电子被加速.A、B是偏向板,使飞进的电子偏离.若已知P、K间所加电压UPK=2.5×103V,偏向板长L=6.0×10-2m,板间距离d=10-2m,所加电压UAB=100V.R=3×10-2m.电子电量为-1.6×10-19C.设从阴极出来的电子速度为零.试问:
如图所示电子射线管阴极K发射电子,阳极P和阴极K间加上电压后电子被加速.A、B是偏向板,使飞进的电子偏离.若已知P、K间所加电压UPK=2.5×103V,偏向板长L=6.0×10-2m,板间距离d=10-2m,所加电压UAB=100V.R=3×10-2m.电子电量为-1.6×10-19C.设从阴极出来的电子速度为零.试问:(1)偏转电场对电子所做的功是多少?
(2)电子最后打在荧光屏上O′点,求OO′间距离是多少?
分析:(1)电子在阳极P和阴极K间运动时,电场力对电子做正功,动能增加,根据动能定理求解电子通过阳极P板的速度υ0.
电子通过偏转电极时做类平抛运动,运用运动的分解:电子沿水平方向做匀速直线运动,竖直方向做匀加速直线运动.根据牛顿第二定律和运动规律求出电子偏转的距离,进而可得偏转电场做的功.
(2)根据速度的分解,求出电子离开偏向板时沿场强方向的分速度vy和偏转角的正切,根据几何知识求解.
电子通过偏转电极时做类平抛运动,运用运动的分解:电子沿水平方向做匀速直线运动,竖直方向做匀加速直线运动.根据牛顿第二定律和运动规律求出电子偏转的距离,进而可得偏转电场做的功.
(2)根据速度的分解,求出电子离开偏向板时沿场强方向的分速度vy和偏转角的正切,根据几何知识求解.
解答:解:
(1)由动能定理:
qUPK=
mv02
解得:
v0=
电子的加速度为:
a=
在电场中的飞行时间为:
t=
出偏转电场时,沿电场方向的分速度为:
vy=at=
故电场力做功为:
W=
mvy2=
×m×(
)2=
=
J=5.76×10-20J
(2)电子出电场中的偏向角满足:
tanθ=
=
电子离开电场时沿场强方向的侧移:
y′=
at2=
×
×(
)2=
故由几何知识得:
y=y′+Rtanθ=
+
=
=
m=1.08×10-2m.
答:
(1)偏转电场对电子所做的功为5.76×10-20J.
(2)电子最后打在荧光屏上O′点,OO′间距离为1.08×10-2m.
(1)由动能定理:
qUPK=
| 1 |
| 2 |
解得:
v0=
|
电子的加速度为:
a=
| qUAB |
| md |
在电场中的飞行时间为:
t=
| L |
| v0 |
出偏转电场时,沿电场方向的分速度为:
vy=at=
| qUABL |
| mdv0 |
故电场力做功为:
W=
| 1 |
| 2 |
| 1 |
| 2 |
| qUABL |
| mdv0 |
| q UAB2L2 |
| 4dUPK |
| 1.6×10-19×1002×(6×10-2)2 |
| 4×10-2×2.5×103 |
(2)电子出电场中的偏向角满足:
tanθ=
| vy |
| v0 |
| UABL |
| 2dUPK |
电子离开电场时沿场强方向的侧移:
y′=
| 1 |
| 2 |
| 1 |
| 2 |
| qUAB |
| md |
| L |
| v0 |
| UABL2 |
| 2UPKd |
故由几何知识得:
y=y′+Rtanθ=
| UABL2 |
| 2UPKd |
| RUABL |
| 2dUPK |
| UABL(L+R) |
| 2UPKd |
| 100×6×10-2(6×10-2+3×10-2) |
| 2×2.5×103×10-2 |
答:
(1)偏转电场对电子所做的功为5.76×10-20J.
(2)电子最后打在荧光屏上O′点,OO′间距离为1.08×10-2m.
点评:本题是带电粒子在电场中偏转的基本题型:先加速后偏转问题,采用的是力学方法,关键是分析电荷运动情况要用到正交分解法.

练习册系列答案
相关题目
磁体和电流之间、磁体和运动电荷之间、电流和电流之间都可通过磁场而相互作用,此现象可通过以下实验证明:
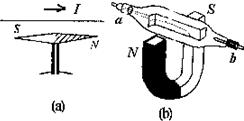
(1)(4分)如图(a)所示,在重复奥斯特的电流磁效应实验时,为使实验方便效果明显,通电导线应_______.
| A.平行于南北方向,位于小磁针上方 |
| B.平行于东西方向,位于小磁针上方 |
| C.平行于东南方向,位于小磁针下方 |
| D.平行于西南方向,位于小磁针下方 |
(2)(4分)如图(b)所示,是一个抽成真空的电子射线管,从阴极发射出来的电子束,在阴极和阳极间的高压作用下,轰击到长方形的荧光屏上激发出荧光,可以显示出电子束运动的径迹.实验表明,在没有外磁场时,电子束是沿直线前进的.如果把射线管放在蹄形磁铁的两极间,荧光屏上显示的电子束运动径迹发生了弯曲,这表明:运动电荷受到了 力,图中a为____极(填阴或阳)
 磁体和电流之间、磁体和运动电荷之间、电流和电流之间都可通过磁场而相互作用,此现象可通过以下实验证明:
磁体和电流之间、磁体和运动电荷之间、电流和电流之间都可通过磁场而相互作用,此现象可通过以下实验证明: