题目内容
2.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处,已知该星球的半径与地球半径之比为R球:R抛=1:4,地球表面重力加速度为g,设该星球表面附近的重力加速度为g′,空气阻力不计.则( )| A. | g′:g=5:1 | B. | g′:g=1:5 | C. | M星:M地=1:20 | D. | M星:M地=1:80 |
分析 竖直上抛运动返回地面时的速度和抛出时的速度大小相等,方向相反,根据匀变速直线运动的规律得出加速度之比,从而得出星球表面的重力加速度.
根据万有引力等于重力求出星球的质量M星与地球质量M地之比.
解答 解:A、B、设竖直上抛小球初速度为v,落回原处时的速度大小为v′,星球表面重力加速度为g′,根据题意知返回地面的速度与抛出时的速度大小相等,方向相反.
地球表面:$t=\frac{-v'-v}{-g}$
星球表面:$5t=\frac{-v'-v}{-g'}$
联解各式得:g'=2m/s2
所以:g′:g=1:5.故A错误,B正确;
C、D、小球在地球或星球表面附近受到的万有引力等于小球重力,得:
星球表面附近:$\frac{{G{M_星}m}}{r^2}=mg'$
地球表面附近:$\frac{{G{M_地}m}}{R^2}=mg$
由题得:$\frac{r}{R}=\frac{1}{4}$
联解各式得:$\frac{M_星}{M_地}=\frac{1}{80}$.故C错误,D正确.
故选:BD
点评 解决本题的关键掌握万有引力等于重力$G\frac{Mm}{{R}^{2}}=mg$,会根据重力加速度之比求出天体的质量之比.

练习册系列答案
相关题目
17.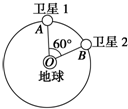 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.如图所示,“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置.若卫星均按顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.如图所示,“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置.若卫星均按顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.如图所示,“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置.若卫星均按顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.如图所示,“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置.若卫星均按顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )| A. | 这两颗卫星的速度大小相等,均为$\sqrt{\frac{r^2}{R}g}$ | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1中质量为m的物体的动能为$\frac{1}{2}$mgr | |
| D. | 卫星1由位置A运动到位置B所需的时间为$\frac{πr}{3R}$ $\sqrt{\frac{r}{g}}$ |
7.关于库仑定律及点电荷,下列说法正确的是( )
| A. | 库仑定律适用于点电荷,点电荷其实就是体积很小的球体 | |
| B. | 当两个带电体的大小及形状对它们之间的相互作用力的影响可以忽略时,这两个带电体可以看成点电荷 | |
| C. | 根据F=$K\frac{{q}_{1}{q}_{2}}{{r}^{2}}$,当两点电荷间的距离趋近于零时,电场力将趋向无穷大 | |
| D. | 若点电荷q1的电荷量大于q2的电荷量,则q1对q2的电场力大于q2对q1的电场力 |
14.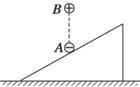 如图所示,可视为点电荷的小球 A、B分别带负电和正电,B球固定,其正下方的A球静止在绝缘斜面上,则( )
如图所示,可视为点电荷的小球 A、B分别带负电和正电,B球固定,其正下方的A球静止在绝缘斜面上,则( )
 如图所示,可视为点电荷的小球 A、B分别带负电和正电,B球固定,其正下方的A球静止在绝缘斜面上,则( )
如图所示,可视为点电荷的小球 A、B分别带负电和正电,B球固定,其正下方的A球静止在绝缘斜面上,则( )| A. | A球一定受到2个力作用 | |
| B. | A球可能受到3个力作用 | |
| C. | A球受到的库仑力方向竖直向上 | |
| D. | A球在B球处产生的场强的方向竖直向上 |
11.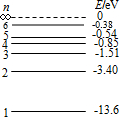 如图所示是氢原子的能级图,用光子能量为12.75eV的光照射一群处于基态的氢原子,可能观测到氢原子发射的不同波长的光有( )
如图所示是氢原子的能级图,用光子能量为12.75eV的光照射一群处于基态的氢原子,可能观测到氢原子发射的不同波长的光有( )
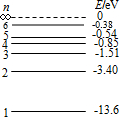 如图所示是氢原子的能级图,用光子能量为12.75eV的光照射一群处于基态的氢原子,可能观测到氢原子发射的不同波长的光有( )
如图所示是氢原子的能级图,用光子能量为12.75eV的光照射一群处于基态的氢原子,可能观测到氢原子发射的不同波长的光有( )| A. | 6种 | B. | 7种 | C. | 10种 | D. | 3种 |
12.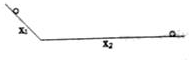 如图所示,一个小球从斜面上由静止匀加速下滑x1,又在水平面上匀减速运动x2后停下,测得x2=3x1,物体在斜面上的加速度大小为a1,在水平面上的加速度大小为a2,则( )
如图所示,一个小球从斜面上由静止匀加速下滑x1,又在水平面上匀减速运动x2后停下,测得x2=3x1,物体在斜面上的加速度大小为a1,在水平面上的加速度大小为a2,则( )
 如图所示,一个小球从斜面上由静止匀加速下滑x1,又在水平面上匀减速运动x2后停下,测得x2=3x1,物体在斜面上的加速度大小为a1,在水平面上的加速度大小为a2,则( )
如图所示,一个小球从斜面上由静止匀加速下滑x1,又在水平面上匀减速运动x2后停下,测得x2=3x1,物体在斜面上的加速度大小为a1,在水平面上的加速度大小为a2,则( )| A. | a1=a2 | B. | a1=2a2 | C. | a1=3a2 | D. | a1=4a2 |


 如图所示,一个质量为10kg的物体,在水推力F的作用下,沿斜面向上匀速运动,已知斜面倾角为37°,物体与斜面间的动摩擦因数为0.5,则水平推力F的大小是200N.
如图所示,一个质量为10kg的物体,在水推力F的作用下,沿斜面向上匀速运动,已知斜面倾角为37°,物体与斜面间的动摩擦因数为0.5,则水平推力F的大小是200N.