题目内容
10.若人造卫星绕地球做匀速圆周运动,则离地面越近的卫星( )| A. | 速度越小 | B. | 角速度越小 | C. | 向心加速度越小 | D. | 周期越小 |
分析 根据万有引力提供向心力得出线速度、角速度、周期、向心加速度与轨道半径的关系,从而比较出大小.
解答 解:根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r=m$\frac{{v}^{2}}{r}$=ma=mω2r,
A、v=$\sqrt{\frac{GM}{r}}$,轨道半径减小,则线速度增大,故A错误;
B、ω=$\sqrt{\frac{GM}{{r}^{3}}}$,轨道半径减小,则角速度越大,故B错误;
C、a=$\frac{GM}{{r}^{2}}$,轨道半径减小,则加速度变大,故C错误;
D、T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,轨道半径减小,则周期越小,故D正确;
故选:D.
点评 解决本题的关键掌握万有引力提供向心力这一理论,知道线速度、角速度、加速度、周期与轨道半径的关系.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
20.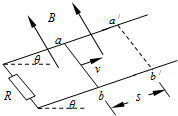 如图示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
 如图示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒受到的最大安培力为$\frac{1}{2R}$B2l2v | |
| B. | 上滑过程中外力对导体棒做的总功为$\frac{1}{2}$mv2 | |
| C. | 上滑过程中电流做功产生的热量为$\frac{1}{2}$mv2-mgs(sinθ+μcosθ) | |
| D. | 上滑过程中导体棒损失的机械能为μmgscosθ |
18.下列速度中,指平均速度的是( )
| A. | 雨滴落地时的速度 | |
| B. | 汽车通过金山大桥的速度 | |
| C. | 子弹射出枪口时的速度 | |
| D. | 跳水运动员起跳后,到达最高点的速度 |
5. 如图所示,汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长.某国产轿车的车轮半径约为30cm,当该型号的轿车在高速公路上行驶时,驾驶员面前速率计的指针指在“120km/h”上,可估算出该车轮的转速约为( )
如图所示,汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长.某国产轿车的车轮半径约为30cm,当该型号的轿车在高速公路上行驶时,驾驶员面前速率计的指针指在“120km/h”上,可估算出该车轮的转速约为( )
 如图所示,汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长.某国产轿车的车轮半径约为30cm,当该型号的轿车在高速公路上行驶时,驾驶员面前速率计的指针指在“120km/h”上,可估算出该车轮的转速约为( )
如图所示,汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长.某国产轿车的车轮半径约为30cm,当该型号的轿车在高速公路上行驶时,驾驶员面前速率计的指针指在“120km/h”上,可估算出该车轮的转速约为( )| A. | 1 000 r/s | B. | 1 000 r/min | C. | 1 000 r/h | D. | 2 000 r/s |
2.关于密闭容器中气体的压强,下列说法正确的是( )
| A. | 气体压强是由于气体分子相互作用产生的 | |
| B. | 气体压强是由于大量气体分子频繁碰撞容器壁产生的 | |
| C. | 气体压强只跟气体分子分子的密集程度有关 | |
| D. | 在完全失重的情况下,密闭容器内的气体对器壁没有压强 |
19.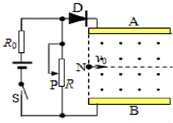 正对着并水平放置的两平行金属板连接在如图电路中,两板间有垂直纸面磁感应强度为B的匀强磁场,D为理想二极管(即正向电阻为0,反向电阻无穷大),R为滑动变阻器,R0为定值电阻.将滑片P置于滑动变阻器正中间,闭合电键S,让一带电质点从两板左端连线的中点N以水平速度v0射入板间,质点沿直线运动.在保持电键S闭合的情况下,下列说法正确的是( )
正对着并水平放置的两平行金属板连接在如图电路中,两板间有垂直纸面磁感应强度为B的匀强磁场,D为理想二极管(即正向电阻为0,反向电阻无穷大),R为滑动变阻器,R0为定值电阻.将滑片P置于滑动变阻器正中间,闭合电键S,让一带电质点从两板左端连线的中点N以水平速度v0射入板间,质点沿直线运动.在保持电键S闭合的情况下,下列说法正确的是( )
 正对着并水平放置的两平行金属板连接在如图电路中,两板间有垂直纸面磁感应强度为B的匀强磁场,D为理想二极管(即正向电阻为0,反向电阻无穷大),R为滑动变阻器,R0为定值电阻.将滑片P置于滑动变阻器正中间,闭合电键S,让一带电质点从两板左端连线的中点N以水平速度v0射入板间,质点沿直线运动.在保持电键S闭合的情况下,下列说法正确的是( )
正对着并水平放置的两平行金属板连接在如图电路中,两板间有垂直纸面磁感应强度为B的匀强磁场,D为理想二极管(即正向电阻为0,反向电阻无穷大),R为滑动变阻器,R0为定值电阻.将滑片P置于滑动变阻器正中间,闭合电键S,让一带电质点从两板左端连线的中点N以水平速度v0射入板间,质点沿直线运动.在保持电键S闭合的情况下,下列说法正确的是( )| A. | 质点可能带正电,也可能带负电 | |
| B. | 若仅将滑片P向上滑动一段后,再让该质点从N点以水平速度v0射入板间,质点运动轨迹一定会向上偏 | |
| C. | 若仅将滑片P向下滑动一段后,再让该质点从N点以水平速度v0射入板间,质点依然会沿直线运动 | |
| D. | 若仅将两平行板的间距变大一些,再让该质点从N点以水平速度v0射入板间,质点运动轨迹会向下偏 |
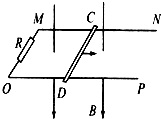 如图所示,电阻不计的平行金属导轨MN和OP水平放置,MO间接有阻值为R的电阻,导轨相距为d,其间有竖直向下的匀强磁场,磁感强度为B.质量为m、电阻为r的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F向右拉动CD,CD受恒定的摩擦阻力f,已知F>f.求:
如图所示,电阻不计的平行金属导轨MN和OP水平放置,MO间接有阻值为R的电阻,导轨相距为d,其间有竖直向下的匀强磁场,磁感强度为B.质量为m、电阻为r的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F向右拉动CD,CD受恒定的摩擦阻力f,已知F>f.求: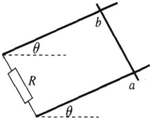 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.(g取10rn/s2,sin37°=0.6,cos37°=0.8)
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.(g取10rn/s2,sin37°=0.6,cos37°=0.8)