题目内容
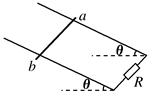
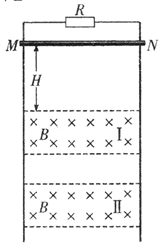
如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距L＝1 m，导轨平面与水平面成θ＝37°角，下端连接阻值R＝2 Ω的电阻．匀强磁场方向与导轨平面垂直．质量m＝0.2 kg、电阻r＝1 Ω的金属棒ab放在两导轨上．棒与导轨垂直并保持良好接触，它们之间的动摩擦因数μ＝0.25(设最大静摩擦力大小等于滑动摩擦力大小)．当金属棒由静止下滑60 m时速度达到稳定，电阻R消耗的功率为8 W，金属棒中的电流方向由a到b，则下列说法正确的是(g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8)( )
| A．金属棒沿导轨由静止开始下滑时，加速度a的大小为 4 m/s2 |
| B．金属棒达到稳定时速度v的大小为10 m/s |
| C．磁场方向垂直导轨平面向上，磁感应强度B的大小为 0.4 T |
| D．金属棒由静止到稳定过程中，电阻R上产生的热量为 25.5 J |
AC
开始下滑时不受安培力，由牛顿第二定律得a＝gsin θ－μgcos θ＝4 m/s2，选项A正确．速度达到稳定时合力为零：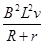
＋μmgcos θ＝mgsin θ，得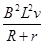＝0.8 N，由已知
·
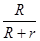＝8 W，得v＝15 m/s，选项B错误．根据左手定则可得，磁场方向垂直于导轨平面向上，由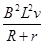＝0.8 N，将v＝15 m/s代入得B＝0.4 T，选项C正确．根据能量守恒，产生的总焦耳热量为Q＝mgxsin θ－
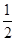mv2－μmgxcos θ＝25.5 J，R上产生的热量为QR＝
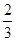Q＝17 J，选项D错误．
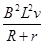＋μmgcos θ＝mgsin θ，得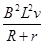＝0.8 N，由已知·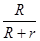＝8 W，得v＝15 m/s，选项B错误．根据左手定则可得，磁场方向垂直于导轨平面向上，由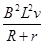＝0.8 N，将v＝15 m/s代入得B＝0.4 T，选项C正确．根据能量守恒，产生的总焦耳热量为Q＝mgxsin θ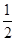－mv2－μmgxcos θ＝25.5 J，R上产生的热量为QR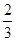＝Q＝17 J，选项D错误．
练习册系列答案
相关题目
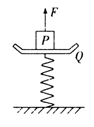
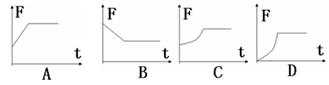
，竖直向下的磁场磁感应强度大小随坐标x的变化关系如图乙所示．开始导体棒CD静止在导轨上的x=0处，现给导体棒一水平向右的拉力，使导体棒以lm/s2的加速度沿x轴匀加速运动，已知导体棒质量为2kg，电阻为2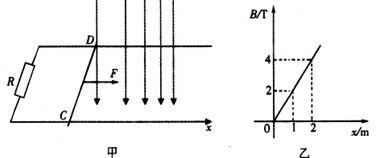
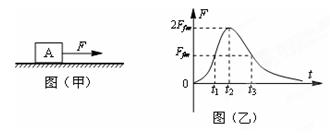
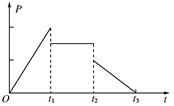
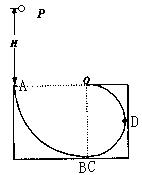
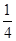圆周轨道，半径OA处于水平位置，CDO是直径为15m的半圆轨道，两个轨道如图连接固定。一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道运动。通过CDO轨道的最低点C时对轨道的压力力等于其重力的
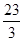倍.取g为10m/s2.
