题目内容
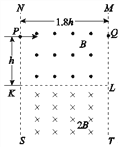
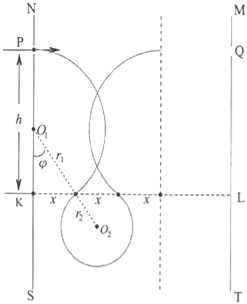
【题目】如图所示，在无限长的竖直边界NS和MT间充满匀强电场，同时该区域上、下部分分别充满方向垂直于NSTM平面向外和向内的匀强磁场，磁感应强度大小分别为B和2B，KL为上下磁场的水平分界线，在NS和MT边界上，距KL高h处分别有P、Q两点，NS和MT间距为1.8h，质量为m，带电荷量为＋q的粒子从P点垂直于NS边界射入该区域，在两边界之间做圆周运动，重力加速度为g.
(1)求电场强度的大小和方向．
(2)要使粒子不从NS边界飞出，求粒子入射速度的最小值．
(3)若粒子能经过Q点从MT边界飞出，求粒子入射速度的所有可能值．
【答案】（1）
，方向竖直向上 （2）
（3）
；
；
【解析】试题分析：（1）粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，电场力与重力合力为零；
（2）作出粒子的运动轨迹，由牛顿第二定律与数学知识求出粒子的速度；
（3）作出粒子运动轨迹，应用几何知识求出粒子的速度．
解：（1）粒子在磁场中做匀速圆周运动，
电场力与重力合力为零，即mg=qE，
解得：E=
，电场力方向竖直向上，电场方向竖直向上；
（2）粒子运动轨迹如图所示：
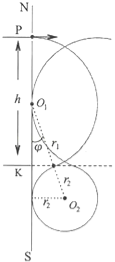
设粒子不从NS边飞出的入射速度最小值为vmin，
对应的粒子在上、下区域的轨道半径分别为r1、r2，
圆心的连线与NS的夹角为φ，
粒子在磁场中做匀速圆周运动，由牛顿第二定律得：
qvB=m
，解得，粒子轨道半径：r=
，
r1=
，r2=
r1，
由几何知识得：（r1+r2）sinφ=r2，r1+r1cosφ=h，
解得：vmin=（9﹣6
）
；
（3）粒子运动轨迹如图所示，
设粒子入射速度为v，
粒子在上、下区域的轨道半径分别为r1、r2，
粒子第一次通过KL时距离K点为x，
由题意可知：3nx=1.8h （n=1、2、3…）
x≥
，x=
，
解得：r1=（1+
）
，n＜3.5，
即：n=1时，v=
，
n=2时，v=
，
n=3时，v=
；
答：（1）电场强度的大小为
，电场方向竖直向上；
（2）要使粒子不从NS边界飞出，粒子入射速度的最小值为（9﹣6
）
．
（3）若粒子经过Q点从MT边界飞出，粒子入射速度的所有可能值为：
、或
、或
．
