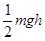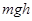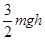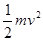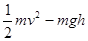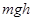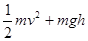题目内容
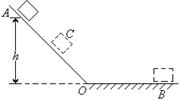
如图所示,质量为m = 2kg的物体,在F = 6N的水平向右的恒力作用下,从A点以V0 = 2m/s的初速度沿着动摩擦因数为0.2的水平轨道AB运动,已知AB = 2m,求:
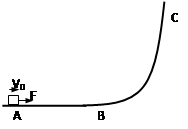
(1)物体在B点的动能;
(2)在B点撤去力F后,如果物体继续沿光滑弧形轨道BC运动,物体在BC段上升的最大高度;
(3)在B点撤去力F后,物体继续沿粗糙弧形轨道BC运动,物体上升的最大高度为0.2 m,则物体在弧形轨道上克服摩擦做的功是多少?(g取10m/s2)
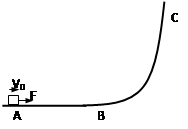
(1)物体在B点的动能;
(2)在B点撤去力F后,如果物体继续沿光滑弧形轨道BC运动,物体在BC段上升的最大高度;
(3)在B点撤去力F后,物体继续沿粗糙弧形轨道BC运动,物体上升的最大高度为0.2 m,则物体在弧形轨道上克服摩擦做的功是多少?(g取10m/s2)
(1)8 J(2)h = 0.4m(3)Wf ="4" J
试题分析:(1)从A到B用动能定理:
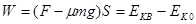 (3分)
(3分)得:
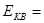 8 J (2分)
8 J (2分)(2)在光滑圆弧上用动能定理:
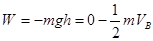 (3分)
(3分)得:h = 0.4m (2分)
(3)在粗糙圆弧上用动能定理:
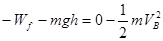 (3分)
(3分)得:Wf ="4" J (2分)
点评:本题难度较小,应用动能定理求解问题时,找到初末状态,进行受力分析和做功分析是关键

练习册系列答案
相关题目
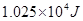
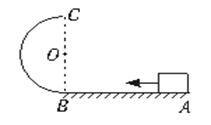
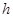 ,物体的质量为m,现将物体m从B点沿原路送回至AO的中点C处,需外力做的功至少应为 ( )
,物体的质量为m,现将物体m从B点沿原路送回至AO的中点C处,需外力做的功至少应为 ( )