题目内容
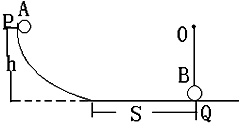 如图示,物体A从高h的p处沿光滑曲面从静止开始下滑,物体B用细线竖直悬挂在O点的钉子上,且刚好与水平面上的Q点接触.物体B可绕钉子在竖直面内运动.曲面上的Q点的水平部分为s.如果物体AB大小形状完全相同且mA=mB,A和B碰撞时无能量损失.求
如图示,物体A从高h的p处沿光滑曲面从静止开始下滑,物体B用细线竖直悬挂在O点的钉子上,且刚好与水平面上的Q点接触.物体B可绕钉子在竖直面内运动.曲面上的Q点的水平部分为s.如果物体AB大小形状完全相同且mA=mB,A和B碰撞时无能量损失.求(1)若水平部分光滑,为使碰撞结束后,物体A做方向向右的匀速直线运动,悬线长L应满足什么条件?
(2)若悬线长L=h,且物体A与水平面间的动摩擦因素为μ,AB可能碰撞多少次?
分析:当水平部分没有摩擦时,A球下滑到未碰B球前能量守恒,与B碰撞因无能量损失,而且质量相等,由动量守恒和能量守恒可得两球交换速度.A 停在Q处,B碰后可能做摆动,也可能饶 O点在竖直平面内做圆周运动.如果做摆动,则经一段时间,B反向与A相碰,使A又回到原来高度,B停在Q处,以后重复以上过程,如此继续下去,若B做圆周运动,B逆时针以O为圆心转一周后与A相碰,B停在Q处,A向右做匀速运动,根据动量守恒定律和能量守恒定律即可求解.
解答:解:(1)A与B碰撞前A的速度:mgh=mvA2,vA=
因为mA=mB,碰撞无能量损失,两球交换速度,得:vA′=0,vB′=vA=
设B球到最高点的速度为v,B做圆周运动的临界条件:mBg=mB
①
又因
mBvB′2=
mBv2+mBg?2L ②
由①②得:L=0.4h
即L≤0.4h时,A、B碰后B才可能做圆周运动,再次碰撞后,物体A做方向向右的匀速直线运动
(2)由上面分析可知,当L=h时,A与B碰后,B只做摆动,因水平面粗糙,所以A在来回运动过程中动能要损失.设碰撞次数为n,由动能定理可得:
mAgh-nmAgS=0
解得:n=
答:(1)若水平部分光滑,为使碰撞结束后,物体A做方向向右的匀速直线运动,悬线长L应满足L≤0.4h;
(2)若悬线长L=h,且物体A与水平面间的动摩擦因素为μ,AB可能碰撞
次.
| 2gh |
因为mA=mB,碰撞无能量损失,两球交换速度,得:vA′=0,vB′=vA=
| 2gh |
设B球到最高点的速度为v,B做圆周运动的临界条件:mBg=mB
| v2 |
| L |
又因
| 1 |
| 2 |
| 1 |
| 2 |
由①②得:L=0.4h
即L≤0.4h时,A、B碰后B才可能做圆周运动,再次碰撞后,物体A做方向向右的匀速直线运动
(2)由上面分析可知,当L=h时,A与B碰后,B只做摆动,因水平面粗糙,所以A在来回运动过程中动能要损失.设碰撞次数为n,由动能定理可得:
mAgh-nmAgS=0
解得:n=
| h+μs |
| 2μs |
答:(1)若水平部分光滑,为使碰撞结束后,物体A做方向向右的匀速直线运动,悬线长L应满足L≤0.4h;
(2)若悬线长L=h,且物体A与水平面间的动摩擦因素为μ,AB可能碰撞
| h+μs |
| 2μs |
点评:本题主要考查了动量守恒定律、能量守恒定律、动能定理的直接应用,要求同学们能正确分析两个小球的运动情况,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,足够长的光滑斜面的倾角为37°,质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连,且mA=3mB.开始时A物体离地高为h=0.5m,物体B恰在斜面底端,从图示位置由静止开始释放A物体,(取g=10m/s2,sin37°=0.6,cos37°=0.8).求:
如图所示,足够长的光滑斜面的倾角为37°,质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连,且mA=3mB.开始时A物体离地高为h=0.5m,物体B恰在斜面底端,从图示位置由静止开始释放A物体,(取g=10m/s2,sin37°=0.6,cos37°=0.8).求: