题目内容
11.汽车在后轮的推动下,以加速度a在地面上沿直线前进,已知汽车前后轮相距为2l,汽车的质心位于前后轮中央,离地高度为h,后轮与地面间的静摩擦系数为μ,前轮非驱动轮,与地面间的摩擦力甚小,可以忽略,试问:μ至少为多大,后轮才不至打滑?并就结果进行讨论.分析 对车受力分析作用受力分析图,根据牛顿第二定律可知加速度与摩擦力的大小关系;再由力矩的平衡条件可明确不打滑的条件.
解答  解:对力受力分析,如图所示;
解:对力受力分析,如图所示;
由牛顿第二定律可知,f=ma
竖直方向有:N1+N2=mg
以前轮为支点;
由力矩平衡可知:
fh+N1l-N2l=0
解得:N1=$\frac{1}{2}$m(g-$\frac{h}{l}a$)
N2=$\frac{1}{2}$m(g+$\frac{h}{l}a$)
要使车不打滑,则有:f≤μN2;
即μ≥$\frac{2al}{gl+ha}$时后轮不会打滑;
讨论可知:
(1)若a>0,N2>N1,后轮对地面压力较大
a=$\frac{l}{h}g$时,N1=0,前轮不受压力;
(3)a>$\frac{l}{h}g$时,N1为负值,不符合实际情况;
(4)a<0时,N1<N2,前轮受力较大;
答:当μ≥$\frac{2al}{gl+ha}$时后轮不会打滑;
点评 本题考查力矩平衡及牛顿第二定律的应用,要注意明确力可以视为绕前轮转动;同时力作用在质心上.

练习册系列答案
相关题目
1. 如图所示为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若小车在平直的公路上以初速度v0开始加速行驶,经过时间t前进的距离为l且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,则此过程中电动机所做的功为( )
如图所示为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若小车在平直的公路上以初速度v0开始加速行驶,经过时间t前进的距离为l且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,则此过程中电动机所做的功为( )
 如图所示为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若小车在平直的公路上以初速度v0开始加速行驶,经过时间t前进的距离为l且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,则此过程中电动机所做的功为( )
如图所示为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若小车在平直的公路上以初速度v0开始加速行驶,经过时间t前进的距离为l且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,则此过程中电动机所做的功为( )| A. | fvmt | B. | Pt | ||
| C. | ft$\frac{{v}_{0}+{v}_{m}}{2}$ | D. | $\frac{1}{2}$mv${\;}_{m}^{2}$+ft-$\frac{1}{2}$mv${\;}_{0}^{2}$ |
2.沪杭高铁在运营前的某次测试中,列车在水平直线轨道上匀速行驶的最大速度为416km/h(约为116m/s).假定列车的总质量为4.40×105 kg.列车以最大速度匀速行驶中时所受的阻力为车重的0.03倍,则此时列车牵引力的功率约为( )
| A. | 5.1×107W | B. | 5.1×108W | C. | 1.5×107W | D. | 1.5×108W |
5.关于曲线运动,下列说法正确的是( )
| A. | 曲线运动一定是变速运动 | |
| B. | 曲线运动速度的方向不断的变化,但速度的大小可以不变 | |
| C. | 曲线运动一定有加速度 | |
| D. | 曲线运动的速度大小和方向一定同时改变 |
3.在用伏安法测电阻实验中,Rx为被测电阻.下面说法正确的是( )
| A. | 当Rv>>Rx时,用外接法 | B. | 当Ra>>Rx用外接法 | ||
| C. | 当Rx>>Ra用内接法 | D. | 当Rx>>Ra用内接法 |
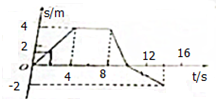 据图回答下列问题:
据图回答下列问题: 如图所示,在升降机中,用水平方向的力将质量为0.2kg的物体压在竖直的墙壁上,物块与墙壁间的动摩擦因数μ=0.4.
如图所示,在升降机中,用水平方向的力将质量为0.2kg的物体压在竖直的墙壁上,物块与墙壁间的动摩擦因数μ=0.4.