题目内容
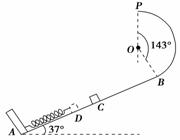
如图,AB为倾角θ=37°的斜面轨道,轨道的AC部分光滑,CB部分粗糙。BP为圆心角等于143°半径R=1 m的竖直光滑圆弧形轨道,两轨道相切于B点,P、O两点在同一竖直线上。轻弹簧一端固定在A点,另一自由端在斜面上C点处,现有一质量m=2 kg的物块在外力作用下将弹簧缓慢压缩到D点后(不拴接)释放,物块经过C点后,从C点运动到B点过程中其位移与时间的关系为x=12t-4t2(式中x单位是m,t单位是s),且物块恰能到达P点。已知sin 37°=0.6,cos 37°=0.8,g=10 m/s2。
(1)若CD=1 m,试求物块从D点运动到C点的过程中,弹簧对物块所做的功;
(2)求B、C两点间的距离x。
(1)由x=12t-4t2知,物块在C点速度为v0=12 m/s …………………………①
设物块从D点运动到C点的过程中,弹簧对物块所做的功为W,
由动能定理得:![]() ……………………………… ②
……………………………… ②
代入数据得:![]() ……………………………… ③
……………………………… ③
(2)由![]() 知,物块从C运动到B过程中的加速度大小为
知,物块从C运动到B过程中的加速度大小为![]() ………………④
………………④
设物块与斜面间的动摩擦因数为μ,由牛顿第二定律得
![]() ⑤
⑤
代入数据解得
![]() ……………………………… ⑥
……………………………… ⑥
物块在P点的速度满足
![]() ……………………………… ⑦
……………………………… ⑦
物块从B运动到P的过程中机械能守恒,则有
![]() …………………………⑧
…………………………⑧
![]() ………………………………⑨
………………………………⑨
物块从C运动到B的过程中有
![]() ………………………………⑩
………………………………⑩
由以上各式解得
![]() ………………………………
………………………………![]()
(其中①③④⑤⑥⑦⑧⑨⑩![]() 式各1分,②式2分,共12分)
式各1分,②式2分,共12分)

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案