题目内容
20. 如图所示a1b1c1d1和a2b2c2d2为在同一竖直平面内的金属导轨,处在磁感应强度为B的匀强磁场中,磁场方向垂直导轨所在平面(纸面)向里.导轨的a1b1段与a2b2段是竖直的,距离为L1,c1d1段与c2d2段也是竖直的,距离为L2,x1y1与x2y2为两根用不可伸长的绝缘轻线相连的金属细杆,质量分别为m1和m2,它们都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R,F为作用于金属杆x1y1上的竖直向上的恒力.已知两杆运动到图示位置时,已匀速向上运动,求此时作用于两杆的重力的功率大小和回路电阻上的热功率.
如图所示a1b1c1d1和a2b2c2d2为在同一竖直平面内的金属导轨,处在磁感应强度为B的匀强磁场中,磁场方向垂直导轨所在平面(纸面)向里.导轨的a1b1段与a2b2段是竖直的,距离为L1,c1d1段与c2d2段也是竖直的,距离为L2,x1y1与x2y2为两根用不可伸长的绝缘轻线相连的金属细杆,质量分别为m1和m2,它们都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R,F为作用于金属杆x1y1上的竖直向上的恒力.已知两杆运动到图示位置时,已匀速向上运动,求此时作用于两杆的重力的功率大小和回路电阻上的热功率.
分析 当两棒匀速向上运动时,以两棒组成的系统为研究对象,拉力F等于重力和安培力之和;由于是两根同时切割磁感线,因此要弄清两根中的电流方向从而求出回路中的电动势.
解答 解 设杆向上运动的速度为v,
此时回路中的电动势:E=B(L2-L1)v ①
回路中的电流:I=$\frac{E}{R}$ ②
根据右手定则电流沿顺时针方向,x1y1受到向上的安培力:F1=BIL1,
金属杆x2y2受到向下的安培力:F2=BIL2,
当杆匀速运动时,根据牛顿第二定律得:
F+F1=(m1+m2)g+F2 ③
联立①②③得:I=$\frac{F-({m}_{1}+{m}_{2})g}{B({L}_{2}-{L}_{1})}$,v=$\frac{FR-({m}_{1}+{m}_{2})gR}{{B}^{2}({L}_{2}-{L}_{1})^{2}}$,
所以作用于两杆的重力的功率为:P=(m1+m2)gv=$\frac{({m}_{1}+{m}_{2})gFR-({m}_{1}+{m}_{2})^{2}{g}^{2}R}{{B}^{2}({L}_{2}-{L}_{1})^{2}}$,
回路电阻上的热功率为:Q=I2R=$\frac{[F-({m}_{1}+{m}_{2})g]^{2}R}{{B}^{2}({L}_{2}-{L}_{1})^{2}}$;
答:此时作用于两杆的重力的功率大小为:$\frac{({m}_{1}+{m}_{2})gFR-({m}_{1}+{m}_{2})^{2}{g}^{2}R}{{B}^{2}({L}_{2}-{L}_{1})^{2}}$,回路电阻上的热功率为:$\frac{[F-({m}_{1}+{m}_{2})g]^{2}R}{{B}^{2}({L}_{2}-{L}_{1})^{2}}$.
点评 这是一道电磁感应中的综合题,对于这类题目要弄清回路中的电流方向和安培力的方向,然后根据平衡或牛顿第二定律求解.

 备战中考寒假系列答案
备战中考寒假系列答案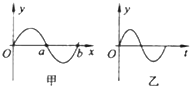
| A. | 当波沿x轴正方向传播时,图乙表示a质点的振动图象 | |
| B. | 当波沿x轴负方向传播时,图乙表示a质点的振动图象 | |
| C. | 当波沿x轴正方向传播时,图乙表示b质点的振动图象 | |
| D. | 当波沿x轴负方向传播时,图乙表示b质点的振动图象 |

| A. | 交变电流的频率f=0.2Hz | |
| B. | 交变电流的有效值I=14.1 A | |
| C. | 交变电流瞬时值表达式 i=20sin0.02t A | |
| D. | 在t=时刻,电流的大小与其有效值相等 |

 如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T.一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离P的距离应为1m (g取10m/s2)
如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T.一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离P的距离应为1m (g取10m/s2)