题目内容
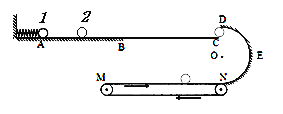
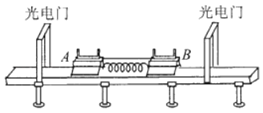
【题目】春节期间同学们玩一种趣味物理游戏,如图所示。选手把玩具电动车放在木板上,电动车在起始线AA处启动向BB前进,游戏规定:玩具车速度为零时离终点线BB越近的成绩越好。为此需要在玩具车运动过程中将木板的右端逐渐抬高。整个运动过程可简化为:玩具电动车启动后,先在水平木板上运动一段时间, 再将木板右端瞬间抬高使之成为倾角为30°的斜面,小车继续沿木板运动。(假设抬高瞬间玩具车速度大小不变,木板左端始终不动,玩具车可看作质点)。已知:电动车质量为0.4kg,运动时能产生2.2N的恒定牵引力,阻力始终是重力的k倍,AB之间距离为4m。试验中发现,若木板始终保持水平,电动车在AA线启动后到达BB的时间为4s。
(1)求出k的数值;
(2)求出玩具车在斜面上运动时加速度的大小;
(3)要让该玩具电动车达到最好成绩,则应在玩具车水平运动多少时间之后瞬间抬高木板。

【答案】(1)0.5;(2)4.5m/s2;(3)![]() s
s
【解析】
(1)若木板始终保持水平,则x=4m,t=4s,由运动学知识
x=![]() a1t2
a1t2
解得a1=0.5m/s2,根据牛顿第二定律
F-kmg=ma1
代入数据解得k=0.5。
(2)玩具车在斜面上运动时,根据牛顿第二定律
![]()
解得玩具车在斜面上运动时加速度的大小a2=4.5m/s2。
(3)玩具车速度为零时恰好到达终点线BB达到最好成绩,设将木板右端瞬间抬高时玩具车的速度为v,则
![]() +
+![]() =x
=x
解得v=![]() m/s,玩具车水平运动的时间
m/s,玩具车水平运动的时间
t=![]() =
=![]() s=
s=![]() s
s
答:(1)k的数值为0.5;
(2)玩具车在斜面上运动时加速度的大小a2=4.5m/s2;
(3)应在玩具车水平运动![]() s之后瞬间抬高木板。
s之后瞬间抬高木板。

练习册系列答案
相关题目