Question

【题目】如图所示，固定于水平桌面上的金属框架cdef处在竖直向下的匀强磁场中，金属棒ab搁在框架上，可无摩擦滑动．此时adeb构成一个边长为l的正方形，棒的电阻为r，其余部分电阻不计．开始时磁感应强度为B0.

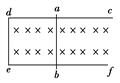
(1)若从t＝0时刻起，磁感应强度均匀增大，每秒增量为k，同时保持棒静止．求棒中的感应电流．在图上标出感应电流的方向；

(2)在上述(1)情况中，棒始终保持静止，当t＝t1 s末时需加的垂直于棒的水平拉力为多少？

(3)若从t＝0时刻起，磁感应强度逐渐减小，当棒以恒定速度v向右做匀速运动时，可使棒中不产生感应电流，则磁感应强度应怎样随时间变化？(写出B与t的关系式)

Answer 1

【答案】(1) ，电流为逆时针方向；(2)(B0＋kt1) 　(3)B＝

【解析】(1)据题意＝k，在磁场均匀变化时，回路中产生的电动势为E＝＝·S＝kl2，由闭合电路欧姆定律知，感应电流为.由楞次定律，判定感应电流为逆时针方向，图略．

(2)t＝t1 s末棒静止，水平方向受拉力F外和安培力F安，F外＝F安＝BIl，又B＝B0＋kt1，

故F外＝(B0＋kt1) .

(3)因为不产生感应电流，由法拉第电磁感应定律E＝，知ΔΦ＝0也就是回路内总磁通量不变，即B0l2＝Bl(l＋vt)，解得B＝.