题目内容
2.如图甲所示,带斜面的足够长木板P,质量M=3kg.静止在水平地面上,其右侧靠竖直墙壁,倾斜面BC与水平面AB的夹角θ=37°、两者平滑对接.t=0s时,质量m=1kg、可视为质点的滑块Q从顶点C由静止开始下滑,图乙所示为Q在0~6s内的速率v随时间t变化的部分图线.已知P与Q间的动摩擦因数是P与地面间的动摩擦因数的5倍,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
(1)木板P与地面间的动摩擦因数.
(2)t=8s时,木板P与滑块Q的速度大小.
分析 根据乙图可知,0-2s内物体做匀加速直线运动,2-6s内做匀减速直线运动,所以0-2s内在斜面上下滑,2-6s内在水平面上滑行,根据v-t图象求出加速度,再根据牛顿第二定律求出动摩擦力因数,进而求出木板P与地面间的动摩擦因数;分别对Q和P运用牛顿第二定律及运动学基本公式求解t=8s时,木板P与滑块Q的速度大小
解答 解:(1)0~2s内,P因墙壁存在而不动,Q沿BC下滑,2s末的速度为v1=10m/s.
设P、Q间动摩擦因数为μ1,P与地面间的动摩擦因数为 μ2,
对Q:由 图象有:a1=$\frac{10}{2}$=5m/s2;
由牛顿第二定律有:mgsin37°-μ1mgcos37°=ma1
联立求解得:μ1=0.125,
则有:μ2=$\frac{0.125}{5}$=0.025
(2)2s后,Q滑到AB上,因 μ1mg>μ2(m+M)g
故P、Q相对滑动,且Q减速、P加速.设加速度大小分别为 a2和a3,Q从B滑到AB上到P、Q共速所用的时间为 t0,
对Q有:μ1mg=ma2
对P有:μ1mg-μ2(m+M)g=Ma3
共速时 v1-a2t0=a3t0
分别求解得:a2=1.25m/s2;
a3=$\frac{1}{12}$m/s2,
t0=7.5s,
故在 t=8s时二者没达相同速度,vQ=10-1.25×6=2.5m/s
vP=a3×6=$\frac{1}{12}$×6=0.5/s
答:(1)木板P与地面间的动摩擦因数为0.025;
(2)t=8s时,木板P与滑块Q的速度大小分别为0.5m/s和2.5m/s
点评 本题抓哟考查了匀变速直线运动及其公式、图象牛顿运动定律、牛顿定律的应用,要求同学们能正确分析物体的运动情况,能根据图象求解加速度和位移,难度较大.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
13. 用单摆测定重力加速度的实验如图1所示.
用单摆测定重力加速度的实验如图1所示.
①组装单摆时,应在下列器材中选用(选填选项前的字母)AD
A.长度为1m左右的细线 B.长度为30cm左右的细线
C.直径为1.8cm的塑料球 D.直径为1.8cm的铁球
②测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t.则重力加速度g=$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$(用 L,n,t 表示)
③表是某同学记录的3组实验数据,并做了部分计算处理.
请计算出第3组实验中的 T=2.01s,g=9.76m/s2
④用多组实验数据做出T2-L图象,也可以求出重力加速度g,已知三位同学做出的T2-L图线的示意图如图2中的a,b,c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值.则相对于图线b,下列分析正确的是(选填选项前的字母)B
A.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值.
 用单摆测定重力加速度的实验如图1所示.
用单摆测定重力加速度的实验如图1所示.①组装单摆时,应在下列器材中选用(选填选项前的字母)AD
A.长度为1m左右的细线 B.长度为30cm左右的细线
C.直径为1.8cm的塑料球 D.直径为1.8cm的铁球
②测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t.则重力加速度g=$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$(用 L,n,t 表示)
③表是某同学记录的3组实验数据,并做了部分计算处理.
| 组次 | 1 | 2 | 3 |
| 摆长L/cm | 80.00 | 90.00 | 100.00 |
| 50 次全振动时间t/s | 90.0 | 95.5 | 100.5 |
| 振动周期T/s | 1.80 | 1.91 | |
| 重力加速度g/(m•s-2) | 9.74 | 9.73 |
④用多组实验数据做出T2-L图象,也可以求出重力加速度g,已知三位同学做出的T2-L图线的示意图如图2中的a,b,c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值.则相对于图线b,下列分析正确的是(选填选项前的字母)B
A.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值.
17. 如图所示,A、B、C、D是真空中一正四面体的四个顶点.现在在A、B两点分别固定两个点电荷Q1和Q2,则关于C、D两点的场强和电势,下列说法正确的是( )
如图所示,A、B、C、D是真空中一正四面体的四个顶点.现在在A、B两点分别固定两个点电荷Q1和Q2,则关于C、D两点的场强和电势,下列说法正确的是( )
 如图所示,A、B、C、D是真空中一正四面体的四个顶点.现在在A、B两点分别固定两个点电荷Q1和Q2,则关于C、D两点的场强和电势,下列说法正确的是( )
如图所示,A、B、C、D是真空中一正四面体的四个顶点.现在在A、B两点分别固定两个点电荷Q1和Q2,则关于C、D两点的场强和电势,下列说法正确的是( )| A. | 若Q1和Q2是等量异种电荷,则C、D两点电场强度不同,电势相同 | |
| B. | 若Q1和Q2是等量异种电荷,则C、D两点电场强度和电势均相同 | |
| C. | 若Q1和Q2是等量同种电荷,则C、D两点电场强度和电势均不相同 | |
| D. | 若Q1和Q2是等量同种电荷,则C、D两点电场强度不相同,电势相同 |
7. 如图所示,质量为m的木块在质量为M的长木板上受到水平向右的拉力F作用向右滑行,长木板处于静止状态.已知木块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2.下列说法正确的是( )
如图所示,质量为m的木块在质量为M的长木板上受到水平向右的拉力F作用向右滑行,长木板处于静止状态.已知木块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2.下列说法正确的是( )
 如图所示,质量为m的木块在质量为M的长木板上受到水平向右的拉力F作用向右滑行,长木板处于静止状态.已知木块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2.下列说法正确的是( )
如图所示,质量为m的木块在质量为M的长木板上受到水平向右的拉力F作用向右滑行,长木板处于静止状态.已知木块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2.下列说法正确的是( )| A. | 木板受到地面的摩擦力的大小一定是μ2mg | |
| B. | 木板受到地面的摩擦力的大小一定是μ1(m+M)g | |
| C. | 无论怎样改变F的大小,木板都不可能运动 | |
| D. | 当F>μ2(M+m)g时,木板发生运动 |
14.质量为m的物体,沿倾角为α的光滑斜面由静止下滑,当下滑t(s)时重力势能减少量为( )
| A. | $\frac{1}{2}$mg2t2sinα | B. | $\frac{1}{2}$mg2t2 | C. | mg2t2 | D. | $\frac{1}{2}$mg2t2sin2α |
11.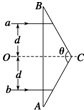 如图所示,ABC为等腰棱镜,两束频率不同、宽度均为d的平行光a和b,分别垂直AB边射向棱镜,棱镜的对称轴OC为两束光的分界线,棱镜对a光和b光的折射率分别为n1和n2,且n1<n2,则( )
如图所示,ABC为等腰棱镜,两束频率不同、宽度均为d的平行光a和b,分别垂直AB边射向棱镜,棱镜的对称轴OC为两束光的分界线,棱镜对a光和b光的折射率分别为n1和n2,且n1<n2,则( )
 如图所示,ABC为等腰棱镜,两束频率不同、宽度均为d的平行光a和b,分别垂直AB边射向棱镜,棱镜的对称轴OC为两束光的分界线,棱镜对a光和b光的折射率分别为n1和n2,且n1<n2,则( )
如图所示,ABC为等腰棱镜,两束频率不同、宽度均为d的平行光a和b,分别垂直AB边射向棱镜,棱镜的对称轴OC为两束光的分界线,棱镜对a光和b光的折射率分别为n1和n2,且n1<n2,则( )| A. | 由玻璃射向真空发生全反射时玻璃对a光的临界角比对b光的小 | |
| B. | 分别从棱镜的BC、AC边射出后,a光的宽度比b光的大 | |
| C. | 在玻璃中a光的光速比b光的小 | |
| D. | 用同一装置做双缝干涉实验时,a光干涉条纹间距比b光的小 |
12. 如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m、电阻为R的导体棒置于导轨上,在水平外力作用下沿导轨以速度v匀速向右滑动,滑动过程中始终保持与导轨垂直并接触良好.已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.下列说法正确的是( )
如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m、电阻为R的导体棒置于导轨上,在水平外力作用下沿导轨以速度v匀速向右滑动,滑动过程中始终保持与导轨垂直并接触良好.已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.下列说法正确的是( )
 如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m、电阻为R的导体棒置于导轨上,在水平外力作用下沿导轨以速度v匀速向右滑动,滑动过程中始终保持与导轨垂直并接触良好.已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.下列说法正确的是( )
如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m、电阻为R的导体棒置于导轨上,在水平外力作用下沿导轨以速度v匀速向右滑动,滑动过程中始终保持与导轨垂直并接触良好.已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.下列说法正确的是( )| A. | 电阻R消耗的功率P=$\frac{{B}^{2}{L}^{2}{v}^{2}}{2R}$ | B. | 电阻R消耗的功率P=μmgv | ||
| C. | 水平外力的大小F=$\frac{{B}^{2}{l}^{2}v}{R}$+μmg | D. | 水平外力的大小F=$\frac{{B}^{2}{l}^{2}v}{R}$-μmg |
 如图所示,竖直放置的平行带电导体板A、B和水平放置的平行带电导体板C、D,B板上有一小孔,从小孔射出的带电粒子刚好可从C、D板间左上角切入C、D板间电场,已知C、D板间距离为d,长为2d,UAB=UCD=U>0,在C、D板右侧存在有一个垂直向里的匀强磁场.质量为m,电量为q的带正电粒子由静止从A板释放,沿直线运动至B板小孔后贴近C板进入C、D板间,最后恰好从D板右边缘进入磁场中.带电粒子的重力不计.求:
如图所示,竖直放置的平行带电导体板A、B和水平放置的平行带电导体板C、D,B板上有一小孔,从小孔射出的带电粒子刚好可从C、D板间左上角切入C、D板间电场,已知C、D板间距离为d,长为2d,UAB=UCD=U>0,在C、D板右侧存在有一个垂直向里的匀强磁场.质量为m,电量为q的带正电粒子由静止从A板释放,沿直线运动至B板小孔后贴近C板进入C、D板间,最后恰好从D板右边缘进入磁场中.带电粒子的重力不计.求: 竖直放置的半径R=80cm的半圆形光滑轨道与水平轨道相连接,连接点为P.质量为m=50g的小球以一定的初速度由水平轨道向左运动,并沿圆轨道的内壁运动到最高点M,如果球A经过N点时速度vN=8m/s,经过M点时对轨道的压力为0.5N.重力加速度g取10m/s2.求:
竖直放置的半径R=80cm的半圆形光滑轨道与水平轨道相连接,连接点为P.质量为m=50g的小球以一定的初速度由水平轨道向左运动,并沿圆轨道的内壁运动到最高点M,如果球A经过N点时速度vN=8m/s,经过M点时对轨道的压力为0.5N.重力加速度g取10m/s2.求: