题目内容
（10分）一劲度系数为k的轻弹簧竖直放置，下端固定在水平地面上。将一质量为2m的物体A放置弹簧上端，A物体静止时弹簧长度为L1，将A物体向下按到弹簧长度为L2，由静止将A物体释放，A物体恰能离开弹簧。将物体A换成质量为m的物体B，并将B物体向下按到弹簧长度为L2处，将B物体由静止释放，求B物体运动过程中离水平地面的最大高度。（已知重力加速度为g）
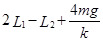
试题分析：物体A静止时，设弹簧的型变量为x ，则
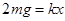（2分）物体A由弹簧长度为L2处开始运动到恰能离开弹簧，设此过程中弹簧减少的弹性势能为ΔEp，由机械能守恒定律得
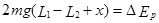（2分）物体B由弹簧长度为L2处开始运动到离开弹簧时速度为v，由机械能守恒定律得
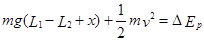（2分）物体B离开弹簧后做竖直上抛运动，其离开弹簧的最大高度为
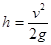（2分）则物体B离水平地面的最大距离为
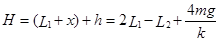（2分）点评：本题难度中等，注意题干中的恰好的的临界条件，在整个系统中只涉及到动能、弹性势能和重力势能，所以系统的机械能守恒，找到几个特殊的状态，分析能量变化是关键
练习册系列答案
相关题目
