题目内容
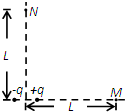 如图,两等量异号的点电荷相距为2a.M与两点电荷共线,N位于两点电荷连线的中垂线上,两点电荷连线中点到M和N的距离都为L,且L?a.略去(
如图,两等量异号的点电荷相距为2a.M与两点电荷共线,N位于两点电荷连线的中垂线上,两点电荷连线中点到M和N的距离都为L,且L?a.略去(| a |
| L |
分析:先根据点电荷的场强公式E=
求解出两电荷单独存在时的场强,再根据平行四边形定则求解出合场强,再运用近似条件比较.
| kq |
| r2 |
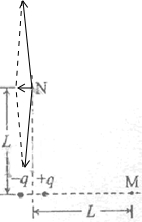
解答:解:如图,根据点电荷的场强公式E=
,运用平行四边形定则,结合结几何关系,M、N点的场强分别为
EM=
-
≈
①
根据相似三角形定则
EN=
≈
②
由①②两式,M点的场强是N点场强的2倍,故A正确,B错误;
由①②两式,M点的场强与N点场强都与a成正比,与L的三次方成反比,故C正确,D错误;
故选AC.
| kq |
| r2 |

EM=
| kq |
| (L-a)2 |
| kq |
| (L+a)2 |
| 4kqa |
| L3 |
根据相似三角形定则
EN=
| kq(2a) | ||
(L2+ a2)
|
| 2kqa |
| L3 |
由①②两式,M点的场强是N点场强的2倍,故A正确,B错误;
由①②两式,M点的场强与N点场强都与a成正比,与L的三次方成反比,故C正确,D错误;
故选AC.
点评:本题关键通过矢量合成求出M与N两点的场强的一般表达式进行讨论.

练习册系列答案
相关题目
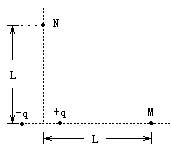 如图,两等量异号的点电荷相距为
如图,两等量异号的点电荷相距为

 项的贡献,则两点电荷的合电场在M和N点的强度:
项的贡献,则两点电荷的合电场在M和N点的强度:
 成正比,方向相反
成正比,方向相反