题目内容
15.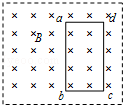 如图所示,在垂直纸面向里的磁感应强度为B的有界矩形匀强磁场区域内,有一个由均匀导线制成的单匝矩形线框abcd,线框平面垂直于磁感线.线框以恒定的速度v沿垂直磁场边界向左运动,运动中线框dc边始终与磁场右边界平行,线框边长ad=l,cd=2l,线框导线的总电阻为R,则线框离开磁场的过程中,下列说法正确的是( )
如图所示,在垂直纸面向里的磁感应强度为B的有界矩形匀强磁场区域内,有一个由均匀导线制成的单匝矩形线框abcd,线框平面垂直于磁感线.线框以恒定的速度v沿垂直磁场边界向左运动,运动中线框dc边始终与磁场右边界平行,线框边长ad=l,cd=2l,线框导线的总电阻为R,则线框离开磁场的过程中,下列说法正确的是( )| A. | 线框离开磁场过程中cd两点间的电势差$\frac{BLv}{3}$ | |
| B. | 线框离开磁场的过程中流过线框截面的电量为$\frac{2B{l}^{2}}{R}$ | |
| C. | 线框离开磁场的过程中产生的热量为$\frac{{8{B^2}{L^3}v}}{R}$ | |
| D. | 线框从图示位置至完全离开磁场的过程中,线框中感应电流方向不变 |
分析 由q=$\frac{△Φ}{R}$求出电荷量,分析磁通量变化量关系,来求解感应电量.分析线框的受力情况,线框所受安培力的合力.
根据焦耳定律求解电流产生的热量.并根据楞次定律来确定感应电流的方向
解答 解:A、线框离开磁场过程中cd两点间的电势差:Ucd=I×$\frac{R}{6l}$×4l=$\frac{B•2l•v}{R}$×$\frac{2}{3}$R=$\frac{4Blv}{3}$,故A错误;
B、线框离开磁场过程流过线框横截面的电荷量:q=I△t=$\frac{E}{R}$△t=$\frac{△Φ}{△t}$$\frac{1}{R}$△t=$\frac{△Φ}{R}$=$\frac{B•l•2l}{R}$=$\frac{2B{l}^{2}}{R}$,故B正确.
C、产生的感应电动势:E=2Blv,感应电流:I=$\frac{E}{R}$,线框中的电流产生的热量:Q=I2Rt=I2•R•2$\frac{l}{v}$=$\frac{8{B}^{2}{l}^{3}v}{R}$,故C正确.
D、根据楞次定律可知,只有离开磁场过程中,回路中才有顺时针方向的感应电流,在磁场中没有离开时,穿过线圈的磁通量不变,则没有感应电流,故D错误.
故选:BC.
点评 该题考查了法拉第电磁感应定律和闭合回路欧姆定律的应用,是一道常规题.要注意题目中线框边长不等,分清楚哪个边在切割磁感线.

练习册系列答案
相关题目
6.在以下的哪些情况中可将物体看成质点( )
| A. | 测量金属密度时的一小块金属 | |
| B. | 对学生骑车姿势进行生理学分析 | |
| C. | 研究火星探测器降落火星后如何调整姿势探测火星的表面 | |
| D. | 研究火星 探测器从地球到火星的飞行轨迹 |
3. 如图所示,斜面体A上的物块P用平行于斜面体的轻弹簧拴接在挡板B上,在物块P上施加水平向右的推力F,整个系统处于静止状态,下列说法正确的是( )
如图所示,斜面体A上的物块P用平行于斜面体的轻弹簧拴接在挡板B上,在物块P上施加水平向右的推力F,整个系统处于静止状态,下列说法正确的是( )
 如图所示,斜面体A上的物块P用平行于斜面体的轻弹簧拴接在挡板B上,在物块P上施加水平向右的推力F,整个系统处于静止状态,下列说法正确的是( )
如图所示,斜面体A上的物块P用平行于斜面体的轻弹簧拴接在挡板B上,在物块P上施加水平向右的推力F,整个系统处于静止状态,下列说法正确的是( )| A. | 物块P与斜面之间不一定存在摩擦力 | |
| B. | 轻弹簧一定被拉长 | |
| C. | 地面对斜面体A一定存在摩擦力 | |
| D. | 若增大推力F,则弹簧弹力一定减小 |
10.一辆以20m/s的速度行驶的汽车,突然采取急刹车,加速度大小为8m/s2,汽车在刹车后的3秒内的位移和3秒时的速度分别为( )
| A. | 24 m,4 m/s | B. | 25 m,4 m/s | C. | 24 m,-4 m/s | D. | 25 m,0 |
20.关于时刻和时间,下列说法正确的是( )
| A. | 1min只能分成60个时刻 | |
| B. | 第4s末就是第5s初,指的是时刻 | |
| C. | 时刻表示时间短,时间表示时间长 | |
| D. | 物体在5s内指的是物体在4s末到5s初这1s的时间 |
7.关于多普勒效应,下列说法正确的是( )
| A. | 利用多普勒效应可以测定运动物体的速度 | |
| B. | 产生多普勒效应的原因是波源频率发生了变化 | |
| C. | 产生多普勒效应的原因是观察者和波源之间发生了相对运动 | |
| D. | 甲、乙两列车相向行驶,两车均鸣笛,且所发生的笛声频率相同,那么乙车中的某旅客听到的甲车笛声频率低于他听到的乙车笛声频率 |
4.以下说法正确的是( )
| A. | 由Q=CU可知,一个电容器的带电量Q跟两极板间电势差U成正比 | |
| B. | 由E=$\frac{F}{q}$可知,电场中某点的电场强度E与F成正比 | |
| C. | 由U=Ed可知,匀强电场中的任意两点间的距离越大,则电势差也越大 | |
| D. | 由EP=qφP可知,对于同一电荷,在电势高处电势能一定大 |
