题目内容
将一单摆装置竖直悬挂于某一深度为h（未知）且开口向下的小筒中（单摆的下部分露于筒外），如图a所示．将悬线拉离平衡位置一个小角度后由静止释放，设单摆振动过程中悬线不会碰到筒壁．本实验的长度测量工具只能测量出筒的下端口到摆球球心之距l，并通过改变l而测出对应的摆动周期．
（1）实验中用游标卡尺测量摆球的直径，游标卡尺的示数如图b所示，则摆球的直径为
（2）实验中用秒表测量单摆30次全振动的时间，秒表的示数如图c所示，则秒表的读数为
（3）利用实验中测得的数据描绘的T2-l关系图象如图d所示，则由图象可知，小筒的深度h=
（1）实验中用游标卡尺测量摆球的直径，游标卡尺的示数如图b所示，则摆球的直径为
20.3
20.3
mm．（2）实验中用秒表测量单摆30次全振动的时间，秒表的示数如图c所示，则秒表的读数为
86.5
86.5
s（3）利用实验中测得的数据描绘的T2-l关系图象如图d所示，则由图象可知，小筒的深度h=
30.0
30.0
cm；当地的重力加速度g=9.86
9.86
m/s2．（π=3.14）（结果保留三位有效数字）分析：（1）游标卡尺主尺与游标尺示数之和是游标卡尺的示数；秒表分针示数与秒针示数之和是秒表的示数；
（2）根据单摆周期公式求出重力加速的表达式．
（3）根据数学知识分析图线斜率与重力加速度的关系，求出g．由纵轴的截距求出h．
（2）根据单摆周期公式求出重力加速的表达式．
（3）根据数学知识分析图线斜率与重力加速度的关系，求出g．由纵轴的截距求出h．
解答：解：（1）由图a所示游标卡尺可知，主尺示数是2cm=20mm，游标尺示数是3×0.1mm=0.3mm，游标卡尺所示是20mm+0.3mm=20.3mm；
（2）由图b所示秒表可知，秒表分针示数是1min，秒针示数是26.5s，则秒表示数是86.5s．
（3）根据单摆的周期公式T=2π
得到，T2=
l+
，根据数学知识可知，
=1.2，代入得到，h=0.30m=30.0cm．图线的斜率k=
=4，k=
，则g=
9.86m/s2．
故答案为：（1）20.3；（2）86.5；（3）30.0，9.86．
（2）由图b所示秒表可知，秒表分针示数是1min，秒针示数是26.5s，则秒表示数是86.5s．
（3）根据单摆的周期公式T=2π
|
| 4π2 |
| g |
| 4π2h |
| g |
| 4π2h |
| g |
| 1.2 |
| 0.3 |
| 4π2 |
| g |
| 4π2 |
| k |
故答案为：（1）20.3；（2）86.5；（3）30.0，9.86．
点评：本题从单摆周期公式得到实验测量原理是关键，根据解析式分析图线的物理意义是惯用的思路．
练习册系列答案
相关题目
将一单摆装置竖直悬挂于某一悬点，其中悬线的上部分在带孔的薄挡板上面（单摆的下部分露于板外），如图（甲）所示，将悬线拉离平衡位置一个小角度后由静止释放，设单摆振动过程中悬线不会碰到挡板，如果本实验的长度测量工具只能测量出挡板到摆球球心之间的距离l，并通过改变l而测出对应的摆动周期T，再以T2为纵轴、l为横轴做出函数关系图象，就可以通过此图象得出悬点到挡板的高度h和当地的重力加速度．
将一单摆装置竖直悬挂于某一深度为h（未知）且开口向下的小筒中（单摆的下部分露于筒外），如图1所示，将悬线拉离平衡位置一个小角度后由静止释放，单摆振动过程中悬线不会碰到筒壁，如果本实验的长度测量工具只能测量出筒的下端口到摆球球心的距离L，并通过改变L而测出对应的摆动周期T，再以T2为纵轴、L为横轴作出T2-L函数关系图象，那么就可以通过此图象得出小筒的深度h和当地的重力加速度g．
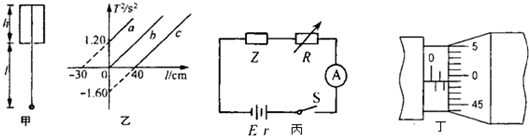
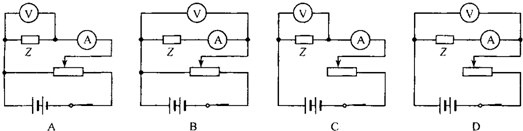
（2011?湖南模拟）将一单摆装置竖直悬挂于某一深度为h（未知）且开口向下的小筒中（单摆的下部分露于筒外），如图1所示，将悬线拉离平衡位置一个小角度后由静止释放，设单摆振动过程中悬线不会碰到筒壁，如果本实验的长度测量工具只能测量出筒的下端口到摆球球心之距L，并通过改变L而测出对应的摆动周期T，再以T2为纵轴、L为横轴作出T2-L函数关系图象，那么就可以通过此图象得出小筒的深度h和当地的重力加速度．